Isogeny, CSIDH, coast
Một bài post nhỏ về isogeny, CSIDH và write-up cho bài coast trong ImaginaryCTF 2024. Do đây là lần đầu tiên mình tiếp cận mảng này (cũng như trình độ có hạn) nên những gì mình viết sẽ theo cách mình hiểu chứ không theo chuẩn logic toán học lắm, mong mọi người thông cảm.
Isogeny
Một cách dễ hiểu thì isogeny gồm 2 thứ:
- Một ánh xạ toàn ánh giữa 2 đường cong Elliptic
- Một đồng cấu nhóm
Trong bài này mình sẽ ký hiệu isogeny $\phi$ từ tập nguồn $E$ vào $E’$ như sau:
\[\phi: E \rightarrow E'\]Ngoài ra thì còn có các thông tin quan trọng như ord, ker, trong bài thì mình thường sẽ gọi ord là bậc (nếu mọi người chưa quen với đường cong Elliptic thì có thể hiểu $\infty$ là phần tử đơn vị nhé):
\[\begin{aligned} \ker\phi &= \{P \in E | \phi(P) = \infty\} \\ ord_\phi &= |\ker\phi| \end{aligned}\]Một vài dòng code để mình có thể dễ hình dung hơn:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
sage: E = EllipticCurve(GF(419), [1, 0]) # Đường cong Elliptic với phương trình y^2 = x^3 + x trên Z mod 419
sage: P = E.random_point()
sage: P # Một điểm P(x, y, z) thuộc E có giá trị như dưới (mọi người chỉ cần quan tâm x, y là đủ)
(297 : 298 : 1)
sage: Q = 84 * P
sage: Q # Tương tự như trên
(349 : 286 : 1)
sage: phi = E.isogeny(Q)
sage: phi # Isogeny bậc 5 ánh xạ từ E: y^2 = x^3 + x -> E': y^2 = x^3 + 269*x + 82 trên Z mod 419 với Q thuộc ker
Isogeny of degree 5 from Elliptic Curve defined by y^2 = x^3 + x over Finite Field of size 419 to Elliptic Curve defined by y^2 = x^3 + 269*x + 82 over Finite Field of size 419
sage: phi(P) # Mọi người có thể kiểm tra 306^2 = 415^3 + 269 * 415 + 82 mod 419
(415 : 306 : 1)
sage: phi(P) + phi(Q) # Do Q thuộc ker nên phi(Q) = inf -> phi(P) + phi(Q) = phi(P)
(415 : 306 : 1)
sage: phi(P + Q) # Isogeny cũng là đồng cấu nhóm nên phi(P + Q) = phi(P) + phi(Q)
(415 : 306 : 1)
sage: 5 * phi(P) # phi(a * P) = a * phi(P) (cũng là đồng cấu nhóm)
(34 : 262 : 1)
sage: phi(5 * P)
(34 : 262 : 1)
sage: phi.degree() # Bậc của phi = số lượng phần tử của ker, ker gồm có các điểm: {(185, 73), (185, -73), (349, 286), (349, -286), inf}
5
Câu hỏi đặt ra, liệu $ord_\phi = 5$ chỉ là ngẫu nhiên?
Câu trả lời là vừa có và vừa không. Có là vì mình đã sử dụng E.random_point() để tạo ra điểm $P$, điểm này có bậc bao nhiêu thì mình không thể đoán trước được, tuy nhiên may mắn thay thì mình sinh được 1 phần tử có bậc bằng với bậc của đường cong $E$.
1
2
sage: P.order()
420
Còn về phần không là do cách mình tạo ra điểm $Q = 84P$. Do $ord_{P} = 420 \rightarrow 420P = \infty \rightarrow 5(84P) = \infty \rightarrow 5Q = \infty$. Vậy $ord_Q = 5$, từ đó $ord_{\phi} = 5$ do $\ker{\phi}$ được sinh bởi $Q$.
Vậy điều gì sẽ xảy ra với $P$ khi nó đi qua $\phi$?
1
2
3
4
5
6
7
8
9
10
sage: phi_P = phi(P)
sage: phi_P.order()
84
sage: Q = 60 * P
sage: phi = E.isogeny(Q)
sage: phi
Isogeny of degree 7 from Elliptic Curve defined by y^2 = x^3 + x over Finite Field of size 419 to Elliptic Curve defined by y^2 = x^3 + 285*x + 87 over Finite Field of size 419
sage: phi_P = phi(P)
sage: phi_P.order()
60
Ta có thể thấy rằng điểm $P, ord_P = d$ thì khi đi qua isogeny $\phi, ord_\phi = q \rightarrow ord_{\phi(P)} = \dfrac{d}{q}$
CSIDH
CSIDH viết tắt cho commutative supersingular isogeny Diffie-Hellman protocol, từ đây ta có thể hiểu CSIDH là một protocol mật mã có sử dụng đến isogeny (các bạn có thể tìm hiểu thêm commutative và supersingular là gì nhé, mình sẽ không viết quá nhiều thứ trong post này).
Nếu bạn quen với crypto thì khi thấy Diffie-Hellman protocol sẽ nghĩ đến bài toán log rời rạc, protocol sẽ diễn ra như sau:
Khóa công khai:
- Một nhóm $G$ hữu hạn
- Một phần tử $g \in G$ có bậc nguyên tố $q$
Khi này Alice sẽ tạo ra khóa bí mật của mình là $a \in Z_{q}$ và gửi cho Bob $g^a$. Bob làm điều tương tự và gửi cho Alice $g^b$. Kết thúc quá trình trao đổi thông tin thì họ sẽ có chung khóa $g^{ab}$. Điểm mấu chốt là do $ab = ba$ (commutative).
Vậy làm thế nào để đưa isogeny vào protocol này?
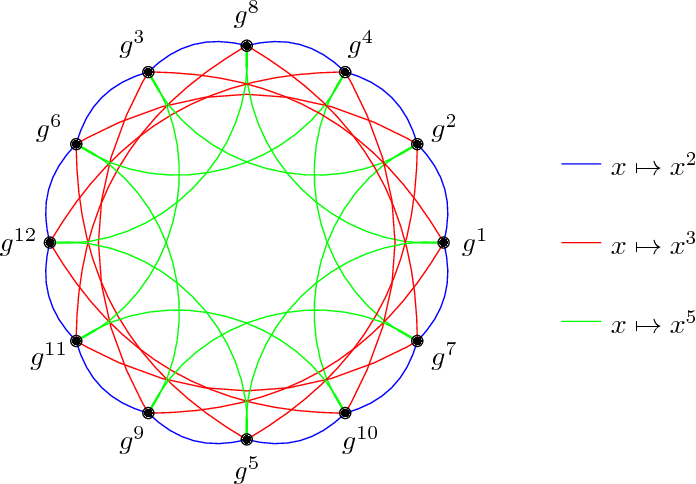
Thay vì lựa chọn các khóa bí mật là các phần tử $a, b$, ta sẽ chọn 2 isogeny $\phi_a, \phi_b$. Ta sẽ hình dung quá trình trao đổi khóa này dưới dạng đồ thị, các đỉnh sẽ là các đường cong Elliptic trong đó đỉnh bắt đầu và đỉnh kết thúc sẽ là khóa công khai còn isogeny sẽ đóng vai trò là các cạnh, các isogeny được Alice và Bob lựa chọn chính là khóa bí mật. Mình sẽ dùng một vài ảnh từ slide bài talk Isogenies: The basics, some applications, and nothing much in between, Lorenz Panny để minh họa (ngoài ra nếu các bạn có hứng thú chủ đề này thì có thể đọc, đây là một trong những slide mình thấy viết dễ hiểu nhất).
Nếu nhìn hình này thì có vẻ quá ít đỉnh, cạnh phải không. Làm sao để có thể bảo mật được?
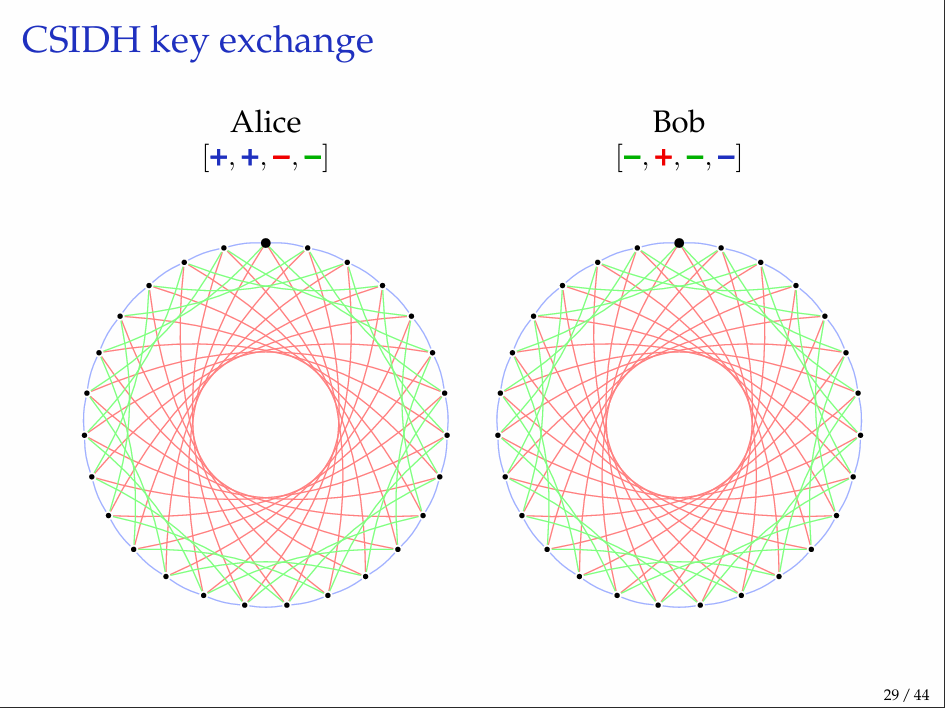
Thay vì đi một lần thì mình hãy đi nhiều lần, đồ thị của ta sẽ trông như sau:
Ở code ban đầu, mình có demo một isogeny bậc 5, ở hình dưới mỗi cạnh xanh dương sẽ là một isogeny bậc 3, màu đỏ là bậc 5 và màu xanh lá là bậc 7. Dấu cộng, trừ cho biết ta cần đi theo chiều xuôi hay nghịch. Mọi người lưu ý là Alice và Bob sẽ cùng xuất phát từ 1 đỉnh, tức cùng 1 đường cong Elliptic. Alice sẽ đi isogeny bậc 3 theo chiều xuôi 2 lần, rồi đi bậc 5, 7 theo chiều nghịch, kết thúc ở một điểm nào đó. Tương tự Bob cũng thế. Sau đó 2 người này trao đổi điểm cho nhau và lặp lại quá trình đi đó và cùng kết thúc ở một điểm giống nhau. Thật là magic.
Một chút code minh họa (các bạn thích thì có thể tìm hiểu thêm về quadratic twist, còn không thì cứ xem nó như thứ cần thiết để đi ngược lại):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
ells = [3, 5, 7, 11, 13, 17]
p = 4 * prod(ells) - 1
F = GF(p)
E = EllipticCurve(F, [1, 0])
a_priv = [4, -2, 1, -3, -2, 1]
b_priv = [1, -1, -2, -3, 1, 2]
# Alice sẽ đi isogeny bậc 3 theo chiều xuôi 4 lần, bậc 5 theo chiều nghịch 2 lần, ...
# Bob sẽ đi isogeny bậc 3 theo chiều xuôi 1 lần, bậc 5 theo chieuf nghịch 1 lần, ...
def compute_isogeny(e, ps, E):
E0 = E
for (ei, pi) in zip(e, ps):
if ei < 0:
for _ in range(abs(ei)):
E0 = E0.quadratic_twist()
Q = E0.random_point() * ((p + 1) // pi) # Cố gắng tạo ra một điểm có bậc pi
while not Q:
Q = E0.random_point() * ((p + 1) // pi)
Q.set_order(pi)
phi = E0.isogeny(Q)
E0 = phi.codomain().quadratic_twist()
else:
for _ in range(ei):
Q = E0.random_point() * ((p + 1) // pi)
while not Q:
Q = E0.random_point() * ((p + 1) // pi)
Q.set_order(pi)
phi = E0.isogeny(Q) # phi: E0 -> E'
E0 = phi.codomain() # Đường cong E'
return E0.montgomery_model().a2(), E0 # Hệ số của đường cong và đường cong
alice_pub, Ea = compute_isogeny(a_priv, ells, E) # public key của Alice
bob_pub, Eb = compute_isogeny(b_priv, ells, E) # public key của Bob
shared_secret, _ = compute_isogeny(a_priv, ells, Eb) # Alice dùng public của Bob và private của mình tạo ra khóa chung
shared_secret2, _ = compute_sogeny(b_priv, ells, Ea) # Bob dùng public của Alice và private của mình tạo ra khóa chung
print(shared_secret2 == shared_secret) # True
Ở phần code trên có đoạn đi theo chiều ngược mình chưa nói rõ, vậy thì cũng giống như đoạn code đầu tiên mình đã demo về việc đi theo chiều xuôi, mình sẽ xem đi theo chiều ngược có những tính chất nào.
1
2
3
4
5
6
7
8
9
10
11
12
13
sage: E = EllipticCurve(GF(419), [1, 0])
sage: E0 = E.quadratic_twist()
sage: P = E0.random_point()
sage: P
(56 : 273 : 1)
sage: P.order()
84
sage: Q = (84 // 7) * P
sage: phi = E0.isogeny(Q)
sage: phi(P)
(210 : 60 : 1)
sage: phi(P).order()
12
Có vẻ như khi đi qua isogeny bậc $7$ thì $ord_P$ cũng bị chia $7$ giống như trường hợp đi theo chiều xuôi. Mọi người để ý rằng điểm $P, Q \in E_0$ chứ không phải $E$ nữa.
1
2
3
4
sage: P in E
False
sage: Q in E
False
Vậy nên nếu như mình tạo ra một điểm $P$ $\in E$ và muốn đi theo chiều ngược thì sẽ bị fail. (Do $\phi$ bây giờ đi từ $E_0 \rightarrow E’$ chứ không phải từ $E$).
Coast
Phần này sẽ là lời giải của mình cho 1 bài liên quan đến CSIDH trong ImaginaryCTF 2024. File gốc nằm ở github của tác giả.
Challenge
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from Crypto.Cipher import AES
from hashlib import sha256
proof.all(False)
# fmt: off
ls = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 929]
# fmt: on
p = 4 * product(ls) - 1
F = GF(p)
E0 = EllipticCurve(F, [1, 0])
G = E0.gen(0)
base = (E0, G)
def keygen():
return [randint(-1, 1) for _ in range(len(ls))]
def exchange(pub, priv):
E, G = pub
es = priv[:]
while any(es):
s = +1 if randint(0, 1) else -1
E.set_order(p + 1)
P = E.random_point()
k = prod(l for l, e in zip(ls, es) if sign(e) == s)
P *= (p + 1) // k
for i, (l, e) in enumerate(zip(ls, es)):
if sign(e) != s:
continue
Q = k // l * P
if not Q:
continue
Q.set_order(l)
phi = E.isogeny(Q)
E, P = phi.codomain(), phi(P)
G = phi(G)
es[i] -= s
k //= l
return E, G
def serialize_pub(pub):
E, G = pub
return (E.a4(), E.a6(), G[0], G[1])
with open("flag.txt", "rb") as f:
flag = f.read().strip()
priv_alice = keygen()
priv_bob = keygen()
pub_alice = exchange(base, priv_alice)
pub_bob = exchange(base, priv_bob)
shared_1 = exchange(pub_alice, priv_bob)
shared_2 = exchange(pub_bob, priv_alice)
assert shared_1 == shared_2
shared_secret = int(shared_1[0].j_invariant() + shared_1[1][0])
key = sha256(str(shared_secret).encode()).digest()
cipher = AES.new(key, AES.MODE_CTR)
ct = cipher.encrypt(flag)
iv = cipher.nonce
base_ser = serialize_pub(base)
pub_alice_ser = serialize_pub(pub_alice)
pub_bob_ser = serialize_pub(pub_bob)
print(f"{base_ser = }")
print(f"{pub_alice_ser = }")
print(f"{pub_bob_ser = }")
print(f"{ct = }")
print(f"{iv = }")
Solution
Nhìn sơ qua thì mình có Alice và Bob trao đổi thông tin dựa trên CSIDH, mình sẽ cần lấy được khóa bí mật của Alice hoặc Bob từ khóa công khai để tìm lại flag.
Ở đây khóa bí mật của Alice và Bob có dạng ${e_1, e_2, \dots, e_k}$ với $k$ là số lượng phần tử trong mảng ls và $-1 \leq e_i \leq 1$
Đối chiếu lại code CSIDH của mình ở mục trước thì mình sẽ nghĩ rằng $e_i = 1$ thì sẽ đi isogeny bậc $ls_i$ $1$ lần theo chiều xuôi, $-1$ thì theo chiều ngược, tuy nhiên code trao đổi khóa (đi isogeny) của tác giả thì có vẻ trông hơi khác, ngoài thông tin về đường cong sau khi đi xong, chúng ta còn được thêm thông tin về điểm $G$ sau khi đi qua các isogeny.
Nếu viết lại hàm exchange của tác giả theo cách viết của mình thì sẽ trông như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def exchange2(pub, priv):
E, G = pub
e = [abs(x) for x in priv]
for (ei, pi) in zip(e, ls):
for _ in range(ei):
Q = E.random_point() * ((p + 1) // pi)
while not Q:
Q = E.random_point() * ((p + 1) // pi)
Q.set_order(pi)
phi = E.isogeny(Q)
E, G = phi.codomain(), phi(G)
return E, G
Hàm exchange của tác giả và hàm exchange2 của mình đều cho kết quả output như nhau. Từ đây mình chắc chắn rằng quá trình đi isogeny của challenge không hề tồn tại chiều nghịch mà chỉ đi theo chiều xuôi. Do đó với mỗi $e_i$ ta chỉ cần quan tâm $0$ hoặc $1$, ta có thể xem giá trị $-1$ như $1$
Tuy nhiên chỉ với nhiêu đây thông tin thì vẫn chưa đủ, nếu mỗi $e_i \in {0, 1}$ thì mình vẫn có $2^k$ trường hợp, không thể brute hết được.
Điều gì sẽ xảy ra với quá trình đi isogeny nếu mình chỉ đi theo chiều xuôi cũng như có thông tin về điểm $G$ sau quá trình đi?
Nhớ lại ở mục Isogeny mình có kết luận như sau:
Điểm $P, ord_P = d$ thì khi đi qua isogeny $\phi, ord_\phi = q \rightarrow ord_{\phi(P)} = \dfrac{d}{q}$
Gọi $G$ là điểm ban đầu và $G_A$ là điểm sau khi Alice đi xong các isogeny của mình. Nếu như $ord_G = d$ thì $ord_{G_A} = \dfrac{d}{\prod{p_i}}$ với $p_i$ là các bậc mà Alice đi. Do mỗi bậc mình chỉ đi tối đa 1 lần, chúng ta có thể xây dựng lại khóa bí mật của Alice như sau:
- Lặp qua từng $p_i$ trong mảng
ls - Kiểm tra xem nếu $ord_{G_A}$ chia hết cho $p_i$
- Nếu có thì $e_i = 1$, không thì $e_i = 0$
Tuy nhiên trong lúc mình làm thì mình thấy việc gọi hàm để tính $ord_{G_A}$ khá lâu nên với mỗi $p_i$ thì mình đi tính điểm $T = \dfrac{d}{p_i} G_A$. Khi này sẽ xảy ra 2 trường hợp:
$T = \infty \rightarrow \dfrac{d}{p_i}$ là bội của $ord_{G_A}\rightarrow$ $p_i$ không có trong phân tích thừa số nguyên tố của $ord_{G_A} \rightarrow$ Alice có đi isogeny bậc $p_i$ $\rightarrow e_i = 1$
Ngược lại $T \not= \infty \rightarrow e_i = 0$
Sau khi có khóa bí mật của Alice thì chúng ta có thể dùng khóa công khai của Bob để tìm lại khóa chung và lấy lại flag.
Solution script
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from Crypto.Cipher import AES
from hashlib import sha256
base_ser = (1, 0, 6395576350626777292729821677181541606370191430555605995902296654660733787961884662675205008112728910627829097716240328518277343733654560980779031197383306195903192278996242667385893559502924064335660043910231897229406366701069814748813352528977494567341233293392314984276702732050363273792561347300313, 4989628161531004318153788074304291273577473031059606908412965124036974844963743869216684686020120111949770513589687750670438648526142795689802013040914101895565898055896213731473214310303864435287131739468789570598441615792162769805326802317670196010077382560220110366549259348962142078308153647899274)
pub_alice_ser = (16796745232047376431076025485853428113133878598097917003461887969217006498108008731966744769172838839455129087919415367459511356804735314320761042839383730282543236466692745670914654548112400401873112245614944913297758267192129423214055383555189748155309668519243823656843679941140887547541583677456851, 8963816826825107706757885015960152371166552220981896678339960705520861493163941960230523020894830135812851365288978634124277530779100695340287569755423459240568704426045331208533913128865584575359563263393253534547084448818884991750356771030230632199257310184446749944357247275509600739836829962695982, 5985363780131483127972578951676841809331634397976984954623788863861777364455401615121494127550821174942018761442458411590922907440513151315213076773138479058971335280960602464177689878904986723530962048747658113657305981717196234378352404797804042544442260172818264948952275310656449986193544911288998, 11649597127875537444034607923163754235537320890125543416303955671947999961428652169037025819875497760380019726767893160005005207635230495183159964997017269895171761165208635703481382384409333096255950930548560628238229917503014555866644994772105200770892341004064761100707021002853325553967825145390381)
pub_bob_ser = (11074315528506118650419974941868902144061087346415910875754699136651403897503986559271837685210876546003254210356095728661380015394250217544836232370667249236726866756134031525443480212922804350247920434230860777321021642812917870058468202706130234985660019235758626667794297106070003964360950607030598, 14788615576129160240974902210621158431820003187709942310686740894110660926275619991889339611525021308542253932884035960214935758630370400596713566372704518819883473808782054060292387578412174017604910767645236213465324157607253511970477802974564062325283523478550237024031582360283010701611159519365278, 14321992806289178321304756176419224025450932661291292547666237239861901427262601709081849960088644959294041693893090273529716185385414362311881174527793744440204632764863112487952716682577231240702585919349036909411205777137409147119242850872654694352308452421920098660171268727320418419754354531076628, 7538734401643277631776877448699813925331537292810845825274725479798688685992383653831671943669387620894416031681699814135234397288844079804264499920949132059399186790837118164550554056080958276489614279355615876249173470199144967698224721556194470026970595690830845832259388888940448493603599827181272)
ct = b'\x8a\x1cs\xa1\xb3\xa77\x81_:\x81\xf8\x83\xc3a\x17\xe1\xd9\xcb\x0c]\x9b\xebP\x06c\x85\x9de1\xeed\x91\x0f\x87_\xf9\x9bD\x7f\xf1\xbdD\x88P\x9eO\x04'
iv = b'\x94j;L,\xf3\xde\xc5'
def keygen():
return [randint(-1, 1) for _ in range(len(ls))]
def exchange2(pub, priv):
E, G = pub
e = [abs(x) for x in priv]
for (ei, pi) in zip(e, ls):
for _ in range(ei):
Q = E.random_point() * ((p + 1) // pi)
while not Q:
Q = E.random_point() * ((p + 1) // pi)
Q.set_order(pi)
phi = E.isogeny(Q)
E, G = phi.codomain(), phi(G)
return E, G
proof.all(False)
ls = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 929]
p = 4 * product(ls) - 1
F = GF(p)
E = EllipticCurve(F, [base_ser[0], base_ser[1]])
E_Alice = EllipticCurve(F, [pub_alice_ser[0], pub_alice_ser[1]])
E_Bob = EllipticCurve(F, [pub_bob_ser[0], pub_bob_ser[1]])
G = E(base_ser[2], base_ser[3])
G_Alice = E_Alice(pub_alice_ser[2], pub_alice_ser[3])
G_Bob = E_Bob(pub_bob_ser[2], pub_bob_ser[3])
a_priv = []
for pi in ls:
T = ((p + 1) // pi) * G_Alice
if T:
a_priv.append(0)
else:
a_priv.append(1)
shared = exchange2((E_Bob, G_Bob), a_priv)
shared_secret2 = int(shared[0].j_invariant() + shared[1][0])
key = sha256(str(shared_secret2).encode()).digest()
cipher = AES.new(key, AES.MODE_CTR, nonce = iv)
flag = cipher.decrypt(ct)
print(flag)
# ictf{just_a_very_broken_implementation_of_csidh}