BackDoorCTF2023
Cuối tuần rồi mình có tham gia chơi BackDoorCTF cùng blackpinker, đây là lời giải của mình cho một vài bài crypto mà mình làm được trong kì thi.
Mini RSA
Script đề bài:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import getPrime , bytes_to_long , GCD
import random
import time
random.seed(time.time())
flag = b"flag{REDACTED}" #Flag has been removed
KEY_SIZE = 512
RSA_E = 3
def fast_exp(a, b, n):
output = 1
while b > 0:
if b & 1:
output = output * a % n
a = a * a % n
b >>= 1
return output
def check(p, q, n):
a_ = random.randint(1, 100)
b_ = random.randint(1, 100)
s = fast_exp(p, fast_exp(q, a_, (p - 1) * (q - 1)), n)
t = fast_exp(q, fast_exp(p, b_, (p - 1) * (q - 1)), n)
result = s + t
print(result)
def gen_RSA_params(N, e):
p = getPrime(N)
q = getPrime(N)
while GCD(e, (p - 1) * (q - 1)) > 1:
p = getPrime(N)
q = getPrime(N)
n = p * q
check(p, q, n)
return (p, q, n)
p, q, n = gen_RSA_params(KEY_SIZE, RSA_E)
m = bytes_to_long(flag)
c = pow(m, RSA_E, n)
print(c)
print(n)
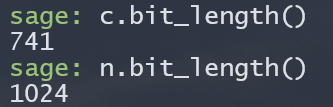
Nhìn chung thì đây là 1 bài RSA với e = 3, check file output thì chúng ta có:
1
2
3
s+t=24986288511406610689718446624210347240800254679541887917496550238025724025245366296475758347972917098615315083893786596239213463034880126152583583770452304
c=5926440800047066468184992240057621921188346083131741617482777221394411358243130401052973132050605103035491365016082149869814064434831123043357292949645845605278066636109516907741970960547141266810284132826982396956610111589
n=155735289132981544011017189391760271645447983310532929187034314934077442930131653227631280820261488048477635481834924391697025189196282777696908403230429985112108890167443195955327245288626689006734302524489187183667470192109923398146045404320502820234742450852031718895027266342435688387321102862096023537079
Đầu tiên mình nhận thấy c khá nhỏ so với n, từ đây mình có thể lấy căn bậc $3$ để thu hồi lại flag
Solve script của mình:
1
2
3
4
5
6
7
8
9
10
from Crypto.Util.number import long_to_bytes as ltb
from sage.all import *
c=5926440800047066468184992240057621921188346083131741617482777221394411358243130401052973132050605103035491365016082149869814064434831123043357292949645845605278066636109516907741970960547141266810284132826982396956610111589
m = ZZ(c).nth_root(3)
print(ltb(m).decode())
# flag{S0_y0u_c4n_s0lv3_s0m3_RSA}
Mini RSA 2
Bài này script cũng tương tự như bài trước, chỉ khác rằng lúc này e = 65537 thay vì e = 3. Bây giờ thì mình không thể sử dụng cách giải cũ nữa, tuy nhiên ở bài trước chúng ta có đại lượng s + t chưa sử dụng đến
Trong đó: $s = p^x$ và $ t = q^y$ với $x, y$ nào đó
Ở đây sẽ có 2 loại:
Bạn là người siêng năng và sẽ chứng minh
s + t = p + qBạn lười như mình và nhận thấy
s + tchỉ có $513$ bits mà $p$ và $q$ đều là các số $512$ bits $\Rightarrow$s + t = p + q
Khi đã có p + q thì mình chỉ cần tính phi = (p - 1) * (q - 1) = n - (p + q) + 1 và lấy flag hoy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import long_to_bytes as ltb
from sage.all import *
st=19238118289292540845900132045328657353776835000175884072088390761517035980189490490459144989703825736320337279576084998885094661611740596902279433080118842
c=8706151122704717355844546946300718218661297718003809762659247903847434328687915436733170976217817899448539289359073472514594584336897461146424215943312922513357040989774130659844482065845748436287563176648482538678604968897565248411495214863860346421741054695295323750935794123435244378357713784569300292101
n=91006417473818125376038413443680810078297391307262694881962992972007772034646331080442026536488576075677538183326514650683359389396367200966050480101000687177953951819685597201494449347363819516742644021041231090322946128861477233797216337306770224218011823327837033401012386386102401543925525885359433574841
print(st.bit_length()) # 513
phi = n - st + 1
e = 65537
d = pow(e, -1, phi)
print(ltb(pow(c, d, n)).decode())
# flag{I_4m_5tuck_0n_Th3_pl4n3t_Eg0_s4ve_M3}
Something in common
Script của đề bài:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
flag = "This flag has been REDACTED"
moduli = "This array has been REDACTED"
m = bytes_to_long(flag.encode())
e = 3
remainders = [pow(m,e,n) for n in moduli]
f = open('output.txt','w')
for i in range(len(moduli)):
f.write(f"m ^ e mod {moduli[i]} = {remainders[i]}\n")
f.write(f"\ne = {e}")
f.close()
Đúng như description, đây là một bài RSA nhưng encrypt m $7$ lần thay vì $1$ lần
Nhìn vào file output ta có:
1
2
3
4
5
6
7
8
9
m ^ e mod 231689896592553079225008346159565141292942746185614335113030628126523977770897610833 = 70932244057518414814271820586538428333420562252483260602196856595136636875881109254
m ^ e mod 7171431858055720778675521 = 6776581747370220150625940
m ^ e mod 66926822362327139196541990168817936306935699 = 48565469191356626147008517582743644359421796
m ^ e mod 437335592290538364420374052921942150635299817629860400585996176158735283605573507708521 = 8794419984130129081066440741470891653922464557881503503363167507918405790466608773101
m ^ e mod 289641633885807692370107575915133663791 = 172864555741817549854149625512946760571
m ^ e mod 667489211907833441904090408183964916738111 = 123698332225047871848637413013333477895868
m ^ e mod 3567528272153764003837574317682649383619949327607 = 2621823962661199268500092259451160990545103771980
e = 3
Ở đây một lần nữa chúng ta gặp lại e = 3, vậy liệu mình có thể sử dụng lại cách như bài Mini RSA hay không?
Thật ra mình cũng chưa check (do mình chả thấy cái $c_i$ nào quá bé so với $n_i$ cả) =))). Nhưng mà mình tận dụng việc tác giả encrypt cùng m $7$ lần bằng cách sử dụng Thặng dư Trung Hoa
Ta sẽ thu được $c \equiv m^3 \pmod{\prod_{i}{n_i}}$. Với $c$ rất bé so với $\prod_{i}{n_i}$, lúc này chúng ta có thể lấy căn bậc $3$ như bài Mini RSA 1 để lấy flag
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sage.all import *
from Crypto.Util.number import long_to_bytes as ltb
mod = [231689896592553079225008346159565141292942746185614335113030628126523977770897610833, 7171431858055720778675521, 66926822362327139196541990168817936306935699, 437335592290538364420374052921942150635299817629860400585996176158735283605573507708521, 289641633885807692370107575915133663791, 667489211907833441904090408183964916738111, 3567528272153764003837574317682649383619949327607]
rem = [70932244057518414814271820586538428333420562252483260602196856595136636875881109254, 6776581747370220150625940, 48565469191356626147008517582743644359421796, 8794419984130129081066440741470891653922464557881503503363167507918405790466608773101, 172864555741817549854149625512946760571, 123698332225047871848637413013333477895868, 2621823962661199268500092259451160990545103771980]
f = crt(rem, mod)
print(product(mod).bit_length()) # 1221
print(ZZ(f).bit_length()) # 1053
print(ltb(ZZ(f).nth_root(3)).decode())
# flag{Wh4t_d0_y0u_m34n_1t_h4s_t0_b3_co-pr1m3}
PRSA
Script của đề bài
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sage.all import *
from Crypto.Util.number import bytes_to_long, getPrime
import random
import time
random.seed(time.time())
message = b'flag{REDACTED}' ## the flag has been removed
F.<x> = PolynomialRing(GF(2), x)
p, q = [F.irreducible_element(random.randint(2 ** 10, 2 ** 12)) for _ in range(2)]
R.<y> = F.quotient_ring(p * q)
n = sum(int(bit) * y ** (len(bin(bytes_to_long(message))[2:]) - 1 - i) for i, bit in enumerate(bin(bytes_to_long(message))[2:]))
e = 2 ** 256
c = n ** e
print(e) ## to be given to the user
print(c) ## to be given to the user
print(p * q) ## to be given to the user
Tiếp tục là $1$ bài về RSA nhưng không dựa vào tập $Z/nZ$ mà chúng ta vẫn hay sử dụng, thay vào đó là trên tập các đa thức $R[x] = GF_2[x]/(p[x] * q[x])$
Cách mình tiếp cận những bài này chính là nghĩ về RSA thông thường chúng ta làm như thế nào rồi chuyển nó về tập mà chúng ta đang xét
RSA thông thường:
Khởi tạo:
Tạo ra một con $n = pq$ với $p$, $q$ là 2 số nguyên tố sao cho từ $n$ chúng ta không thể phân tích ngược lại $p$ và $q$
Encryption:
Giả sử chúng ta muốn encrypt plaintext $m$, chúng ta sẽ đi tính $c \equiv m^e \pmod{n}$. Lúc này $c$ chính là ciphertext
Decryption:
Tính $d$ sao cho $ed \equiv 1 \pmod{\phi(n)}$ với $\phi(n)$ chính là phi hàm Euler của $n$ (ta cần tính $\phi(n)$ là do $a^{\phi(n)} \equiv 1 \pmod{n}$ $\forall a$ sao cho $(a, n) = 1$)
Lúc này ta sẽ có thể decrypt $c$ và thu lại $m$ như sau: $m \equiv c^d \pmod{n}$
Vậy vì sao RSA thông thường an toàn?
Đó là do chúng ta không thể phân tích được $p$ hay $q$ từ $n$. Tuy nhiên trong bài toán mà chúng ta đang xét, từ đa thức $p * q$, chúng ta có thể dễ dàng phân tích ngược lại đa thức $p$, $q$
Việc tiếp theo mà chúng ta cần làm chính là tính xem $\phi(n)$ (từ đây mình sẽ gọi nó là bậc của $R[x]$) bằng bao nhiêu?
Và từ đây mình xin phép giới thiệu
Ngu lần 1
Mình đã đi tính bậc 1 cách ngây thơ đó chính là sử dụng hàm .order() trong sage
Lúc này mình nhận thấy bậc mà mình đã tính ra chia hết cho $e$, tức $(o, e) \neq 1$ mà như vậy thì làm sao mình có thể tạo ra con $d$ như lúc làm bình thường được? Thế là mình đã thử rất nhiều attack khác nhau đến khi mình bí ý tưởng thì mình mới check lại xem bản thân đã tính bậc đúng chưa.
Bạn có nhận ra mình sai ở đâu không =))
Đúng là mình đã tính bậc đúng, nhưng là bậc đối với phép cộng chứ không phải là phép nhân mà mình đang cần tìm lmaoooo.
Sau đó mình đã tính lại bằng hàm .multiplicative_order() thay vì .order() và nhận được dòng lỗi:
AttributeError: 'PolynomialQuotientRing_generic_with_category' object has no attribute 'multiplicative_order'
Vậy là trong sage không có cài đặt sẵn tính bậc đối với phép nhân trong PolynomialQuotientRing. Mình đành lên mạng tra công thức tính
Qua đó mình biết bậc mình cần tính o = lcm([2^p.degree() - 1, 2^q.degree() - 1])
Check lại (sai nữa thì ko biết nói gì, skill issue cực mạnh):
Hên quá nó đúng rồi =)))
Mình đã có hết mọi con số mình cần rồi, giờ thì lấy flag thui :p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from sage.all import *
from Crypto.Util.number import bytes_to_long, getPrime, long_to_bytes as ltb
import random
import time
F.<x> = PolynomialRing(GF(2), x)
pq = F(x^4547 + x^3524 + x^3518 + x^3517 + x^3512 + x^1072 + x^1070 + x^1041 + x^1035 + x^49 + x^47 + x^43 + x^42 + x^41 + x^40 + x^37 + x^35 + x^18 + x^11 + x^5 + 1)
# Factor p*q -> p, q
p, q = F(x^1035 + x^12 + x^6 + x^5 + 1), F(x^3512 + x^37 + x^35 + x^6 + 1)
R.<y> = F.quotient_ring(p * q)
Rp.<rp> = F.quotient_ring(p)
Rq.<rq> = F.quotient_ring(q)
c = ...
e = 115792089237316195423570985008687907853269984665640564039457584007913129639936
M = lcm([2^p.degree() - 1, 2^q.degree() - 1])
d = pow(e, -1, M)
dec = (c ** d).list()[::-1]
t = "".join(str(i) for i in dec)
from Crypto.Util.number import long_to_bytes as ltb
print(ltb(int(t, 2)).decode())
# flag{S0_1mPL3m3n71nG_R54_0n_P0lYn0m1aL5_1n5734d_d1dn7_w0rk_hUh!!?}
Knapsack
Script đề bài:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import random
import hashlib
from Crypto.Util.number import bytes_to_long
from Crypto.Cipher import AES
flag = b"The flag has been REDACTED"
secret = b"The seccret has been REDACTED"
key = hashlib.sha256(secret).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
padded_flag = flag + b'\x00'*(-len(flag)%16)
ciphertext = cipher.encrypt(padded_flag)
f = open('output.txt','w')
f.write(f"Ciphertext: {ciphertext.hex()}\n\n")
arr = [ random.randint(1,1000000000000) for i in range(40) ]
k = bytes_to_long(secret)
s = 0
for i in range(40):
if k&(1<<i):
s+=arr[i]
f.write(f'numbers: {str(arr)[1:-1]}\nsum: {s}\n')
f.close()
Đọc một chút thì chúng ta sẽ biết rằng mục tiêu của bài sẽ là đi tìm secret
Ở đây thì phương trình có liên quan đến secret chính là
Trong đó thì $b_i \in {0, 1}$ chính là bit thứ $i$ của secret, còn arr chính là mảng các số được random mà đề đã cho chúng ta.
Vậy thì mục tiêu của chúng ta sẽ là xác định $b_i$ $(0 \leq i \leq 39)$ từ arr và s. Sau đó thì ta có thể lấy lại secret
Nhìn chung thì đây là 1 bài subset sum cơ bản, chúng ta sẽ dùng LLL để giải bài này
Ở đây thì mình sẽ dùng script trong lbc_toolkit của Joseph (goated tool)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
def subset_sum(weights, targets, modulus=None, N=None, lattice_reduction=None, verbose=False):
verbose = (lambda *a: print('[subset_sum]', *a)) if verbose else lambda *_: None
if type(weights[0]) is list:
k = len(weights)
n = len(weights[0])
else:
k = 1
n = len(weights)
weights = [weights]
targets = [targets]
if modulus is not None:
density = n / (k * log(modulus, 2))
else:
density = n / (k * log(max(flatten(weights)), 2))
verbose('Density:', round(density.n(), 4))
N = N or ceil(sqrt((n+1)/4))
B = 2 * Matrix.identity(n)
B = B.augment(vector([0] * n))
for j in range(k):
B = B.augment(vector([N * a for a in weights[j]]))
if modulus is not None:
B = B.stack(Matrix.zero(k, n + 1).augment(N * modulus * Matrix.identity(k)))
B = B.stack(vector([1] * (n + 1) + [N * s for s in targets]))
verbose('Lattice dimensions:', B.dimensions())
lattice_reduction_timer = cputime()
if lattice_reduction:
B = lattice_reduction(B)
else:
B = B.LLL()
verbose(f'Lattice reduction took {cputime(lattice_reduction_timer):.3f}s')
for row in B:
if row[n] < 0:
sol = [ZZ((x + 1)//2) for x in row[:n]]
else:
sol = [ZZ((1 - x)//2) for x in row[:n]]
if any(x not in [0, 1] for x in sol):
continue
for j in range(k):
t = sum(ZZ(e) * ZZ(a) for e, a in zip(sol, weights[j]))
tj = targets[j]
if modulus > 0:
t %= modulus
tj %= modulus
if t != tj:
break
else:
return sol
return None
numbers = [600848253359, 617370603129, 506919465064, 218995773533, 831016169202, 501743312177, 15915022145, 902217876313, 16106924577, 339484425400, 372255158657, 612977795139, 755932592051, 188931588244, 266379866558, 661628157071, 428027838199, 929094803770, 917715204448, 103431741147, 549163664804, 398306592361, 442876575930, 641158284784, 492384131229, 524027495955, 232203211652, 213223394430, 322608432478, 721091079509, 518513918024, 397397503488, 62846154328, 725196249396, 443022485079, 547194537747, 348150826751, 522851553238, 421636467374, 12712949979]
sum = 7929089016814
print(subset_sum(numbers, sum, verbose=True))
Tuy nhiên trái ngược lại với mong đợi, mình đã không tìm được $b_i$
1
2
3
4
[subset_sum] Density: 1.0061
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.015s
None
Lúc này mình nhận ra rằng density của mảng quá cao so với thuật toán mà mình đang sử dụng
Cụ thể trong tutorial.pdf của Joseph có note rằng:
Rõ ràng $1.0061 > 0.9408$ cho nên có thể đây là lý do mà mình không LLL ra được đáp án, vậy thì tới đây các bạn sẽ làm gì?
Đối với mình thì mình sẽ đưa nó về những gì mình biết để giải :D. Mình không biết cách nào để giải bài knapsack density cao cả, do thế mình sẽ cố gắng khiến cho density thấp xuống. Vậy thì density được tính như thế nào?
Nhìn lại trong script của hàm subset_sum ta có:
1
density = n / (k * log(max(flatten(weights)), 2))
Ở đây mình thấy density sẽ phụ thuộc vào $n$, $k$ và max($arr_i$) $n$, $k$ là $2$ số cố định rồi, vì thế mình chỉ có thể thay đổi các số trong arr. Tuy nhiên chúng ta sẽ phải thay đổi như thế nào?
Cách 1:
Mình sẽ nhân tất cả phần tử của arr một lượng scale_factor nào đó sao cho density mình đủ nhỏ để giải. Khi này mình tự gen số và nhận thấy cách này cũng không cho mình đáp án mà mình mong muốn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
scale_factor = 100000
arr = [ randint(1,1000000000000) for i in range(40) ]
arr_ = [scale_factor * x for x in arr]
for i in range(len(arr)):
assert arr[i] * scale_factor == arr_[i]
k = bytes_to_long(secret)
s = 0
s_ = 0
ans = [0 for i in range(40)]
for i in range(40):
if k&(1<<i):
s+=arr[i]
s_ += arr_[i]
ans[i] = 1
print(f"Wanted: {ans}")
sol = subset_sum(arr_, s_, verbose=True)
print(sol)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0]
[subset_sum] Density: 0.7087
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.018s
None
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1]
[subset_sum] Density: 0.7087
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.021s
None
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1]
[subset_sum] Density: 0.7085
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.019s
None
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1]
[subset_sum] Density: 0.7084
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.015s
None
Do đó mình đã nghĩ thêm cách khác
Cách 2
Do density chỉ phụ thuộc vào số lớn nhất trong trong arr, do đó mình sẽ thử chỉ thay đổi một vài số, tuy nhiên mình cần chọn những số không được cộng vào trong s, vì nếu như cộng vào trong s thì mình sẽ phải thay đổi s nhưng lúc làm bài thật thì làm sao mà mình biết được số nào được cộng và số nào không (mình đang đi tìm điều đó mà :D).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
secret = randbytes(5)
key = hashlib.sha256(secret).digest()[:16]
arr = [ randint(1,1000000000000) for i in range(40) ]
k = bytes_to_long(secret)
s = 0
ans = [0 for i in range(40)]
cnt = 0
for i in range(40):
if k&(1<<i):
s+=arr[i]
ans[i] = 1
elif cnt < 10:
arr[i] = 2^640
cnt += 1
print(f"Wanted: {ans}")
sol = subset_sum(arr, s, verbose=True)
print(sol)
Ở đây mình đã chọn 10 số đầu tiên không nằm trong tổng thành $2^{640}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1]
[subset_sum] Density: 0.0625
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.030s
[1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1]
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
[subset_sum] Density: 0.0625
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.034s
None
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
[subset_sum] Density: 0.0625
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.033s
None
(sage) elita@tehoang:/mnt/d/CTF/practice/idk/WU$ python3 test-knapsack.sage.py
Wanted: [0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1]
[subset_sum] Density: 0.0625
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.035s
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1]
Lúc thì ra kết quả, lúc thì không :D. Tuy nhiên như vậy là quá đủ so với 1 đứa như mình, mình thử luôn cách này cho bài mình đang làm nào :D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import itertools
poss = itertools.combinations(range(40), 4)
poss = list(poss)
t = 1
for cur_comb in poss:
print(t)
nums = [x for x in numbers]
for a in cur_comb:
nums[a] = 2 ** 640
x = subset_sum(nums, sum, verbose=True)
if x != None:
print(x)
break
t += 1
Như mình đã nói, lúc làm bài thật thì mình sẽ không biết những vị trí nào không được cộng vào trong tổng, do đó mình sẽ phải tạo ra tổ hợp các index để thay từ từ. Ở đây mình chọn thay 4 vị trí.
Chạy tới lần 305 thì mình đã có 1 vector thỏa yêu cầu :D
1
2
3
4
5
305
[subset_sum] Density: 0.0625
[subset_sum] Lattice dimensions: (41, 42)
[subset_sum] Lattice reduction took 0.033s
[0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0]
Decrypt lấy flag thôi :D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
t = [0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0]
from Crypto.Util.number import long_to_bytes as ltb
secret = "".join(str(x) for x in t[::-1])
secret = int(secret, 2)
secret = ltb(secret)
key = hashlib.sha256(secret).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
print(cipher.decrypt(bytes.fromhex(Ciphertext)))
# flag{N0t_r34dy_f0r_M3rkl3-H3llman}
ColL3g10n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from hashlib import md5, sha256
import random
from Crypto.Util.number import *
alphanum = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
flag = "This flag has been REDACTED"
secret = ''.join(random.choices(alphanum,k=10))
sec_num = bytes_to_long(secret.encode())
history = []
tries = 3
while tries:
print(f"Tries left : {tries}")
print("Provide the hex of first message: ",end='')
m1 = bytes.fromhex(input())
print("Provide the hex of second message: ",end='')
m2 = bytes.fromhex(input())
if m1==m2:
print("Do you take me as a fool?. Give me 2 different messages.\n")
tries-=1
continue
if m1[0] in history or m2[0] in history:
print("You have already provided messages with the same first byte. You still lose a try.\n")
tries-=1
continue
if md5(m1).hexdigest()==md5(m2).hexdigest() and sha256(m1).hexdigest()[:5]==sha256(m2).hexdigest()[:5]:
history.append(m1[0])
print("Wow! Both messages have the same signature.")
print("Okay I can reveal some part of the secret to you. Give me a number with no more than 24 set bits and I will reveal those bits of the secret to you.")
print("num: ",end='')
num = int(input())
bit_count = bin(num).count('1')
if bit_count>24:
print("Read the rules properly. No more than 24 bits allowed.\n")
tries-=1
continue
print(f"Revealing bits : {sec_num&num}\n")
tries-=1
continue
else:
print("The signatures don't match.\n")
tries-=1
continue
print("Can you Guess the secret: ",end='')
guess = input()
if guess == secret:
print(f"You gussed correctly. Here is your flag: {flag}")
else:
print(f"Wrong guess. Bye bye!")
Đây là một bài hash collision. Cụ thể chúng ta sẽ cần phải collision 1 lần, mỗi lần là 1 cặp (m0, m1) sao cho md5(m1).hexdigest()==md5(m2).hexdigest() and sha256(m1).hexdigest()[:5]==sha256(m2).hexdigest()[:5] cùng thời cùng với đó, byte đầu tiên của cặp sau phải những cặp trước
1
2
3
4
if m1[0] in history or m2[0] in history:
print("You have already provided messages with the same first byte. You still lose a try.\n")
tries-=1
continue
Chắc cái này để không cho chúng ta chơi 1 cặp 3 lần thôi chứ không có gì
Mỗi lần mình collision thành công thì đề sẽ cho mình biết tối đa là 24 bits của secret. Tới đây thì mình check xem secret khoảng bao nhiêu bits.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
In [8]: def lmao():
...: secret = ''.join(random.choices(alphanum,k=10))
...: sec_num = bytes_to_long(secret.encode())
...: return sec_num.bit_length()
...:
In [9]: print(lmao())
78
In [10]: print(lmao())
79
In [11]: print(lmao())
79
In [12]: print(lmao())
79
In [13]: print(lmao())
79
Hmm vậy là khoảng $79$ bits, vậy mình có thể có $24 * 3 = 72$ bits, vậy mình còn $7$ bits chưa biết. Tới đây thì chiến thuật của mình là lấy các bits từ trái sang phải, còn lại $7$ bits cuối cùng không biết thì mình ngồi test local xem cái nào có khả năng xuất hiện nhiều rồi quất cái đó luôn =))). Mình sẽ remote server tới khi nó đúng thì thôi. Ở đây mình đã chọn $7$ bits cuối cùng của mình là 0110000
- Fun fact: lúc làm bài mình đã nhận ra rằng mình có thể biết đến $73$ bits do bits đầu tiên sẽ luôn luôn là $1$, vì thế mình không cần phải lấy bits đầu tiên nữa, với điều này thì chúng ta chỉ còn lại $6$ bits chưa biết. Tuy nhiên mình lại nhận thấy chưa biết $6$ hay chưa biết $7$ thì cũng không ảnh hưởng quá nhiều tới tốc độ ra đáp án đúng, thậm chí có những lúc chọn $7$ bits như mình ở trên cho ra output đúng nhanh hơn cả $1$ vài $6$ bits bất kì
Nói đủ rồi giờ mình exploit thôi =)))
Cái chính của bài này vẫn là phần hash collision. Từ trước đến giờ mình vẫn luôn luôn xem MD5 như 1 block cipher, tức là output của state hiện tại sẽ phụ thuộc vào state trước và nếu như mình có 1 cặp (m0, m1) sao cho md5(m0) = md5(m1) và độ dài của m0, m1 vừa đủ số nguyên lần block (tức là bội của 64 bytes) thì mình có quyền pad thêm 1 đoạn s và vẫn sẽ có được md5(m0 + s) = md5(m1 + s). Tới đây thì mình chỉ cần random s đến khi nào thỏa mãn điều kiện phía sau tức sha256(m1).hexdigest()[:5]==sha256(m2).hexdigest()[:5]. Đây chỉ là 5 characters hexa nên brute cũng khá nhanh thôi. Lúc làm bài thì mình đã sử dụng Hashclash trước để tìm m0, m1 sao cho cùng MD5. Có rồi thì brute như trên hoy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from hashlib import md5, sha256
import os
# Từ hashclash
with open('../collision1.bin', "rb") as f:
a = f.read()
with open('../collision2.bin', "rb") as f:
b = f.read()
assert len(a) == len(b) and len(a) % 64 == 0 and a != b
assert md5(a).hexdigest() == md5(b).hexdigest()
s = os.urandom(5)
while sha256(a + s).hexdigest()[:5] != sha256(b + s).hexdigest()[:5]:
s = os.urandom(5)
a += s
b += s
assert md5(a).hexdigest() == md5(b).hexdigest() and sha256(a).hexdigest()[:5] == sha256(b).hexdigest()[:5]
print("OK found")
Mình làm 3 lần như vậy, mỗi lần nhớ để byte đầu tiên khác đi, sau đó chỉ cần lấy bits rồi remote tới khi nó đúng hoy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from pwn import *
from Crypto.Util.number import *
import random
alphanum = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
a1 = ['5445535440b011627e6079b6b165aa0273d88817f6b3b8b2d9222354701611a383cbba524286e64db3875fd151455dfb3abc096cc945863e2efda21b6e327dc9422703cbcf694a9bcf60fe1537b0ff74e3f93c3529352c27680b2120306805091ba661f6685dc46276f99b6afd5269a4cb02059cef0403e44ab21e2d14eef4f5d4be745763de0e5f76a00caa763bf540', '4553545429080e76bdbee8adef684aafec31abae8ea74d2b26a84cb9d0ea89cb499b553ad309d01c93b332390c5577badc8aff68cb7083222cc4de5f23619139075c99bfbfe65724bc5bc4c8c51ac0305b92ab0697fa5c11b11a1f7a419b4fb212af0926a8081988115c77bfe3eb1b80533fbbf7974f80e3135cc022b4328a5c062d8c76b899c83c68c11b0675ae0ef6', '53455454ea2e55fec1696eb5388dd93dd326b9127b4a8402ce72d8e02bf19baaacf96f40276dcb0b44a6b401a83547e3fd89d53d183084ff4e009bffabcf9bc642c1528901b6a6a014bdd783547555ced1d946b9a13aae4fc2b4103e06355a76e10d0ac2ccfe0563cffe0a4a785f2ceaa602081303ca229445cd2055bf4b5361a1fb148bca069a131dbc518ad0a4e205']
b1 = ['5445535440b011627e6179b6b165aa0273d88817f6b3b8b2d9222354701611a383cbba524286e64db3875fd151455dfb3abc096cc945863e2efda21b6e327dc9422703cbcf694a9bcf5ffe1537b0ff74e3f93c3529352c27680b2120306805091ba661f6685dc46276f99b6afd5269a4cb02059cef0403e44ab21e2d14eef4f5d4be745763de0e5f76a00caa763bf540', '4553545429080e76bdbfe8adef684aafec31abae8ea74d2b26a84cb9d0ea89cb499b553ad309d01c93b332390c5577badc8aff68cb7083222cc4de5f23619139075c99bfbfe65724bc5ac4c8c51ac0305b92ab0697fa5c11b11a1f7a419b4fb212af0926a8081988115c77bfe3eb1b80533fbbf7974f80e3135cc022b4328a5c062d8c76b899c83c68c11b0675ae0ef6', '53455454ea2e55fec16a6eb5388dd93dd326b9127b4a8402ce72d8e02bf19baaacf96f40276dcb0b44a6b401a83547e3fd89d53d183084ff4e009bffabcf9bc642c1528901b6a6a014bcd783547555ced1d946b9a13aae4fc2b4103e06355a76e10d0ac2ccfe0563cffe0a4a785f2ceaa602081303ca229445cd2055bf4b5361a1fb148bca069a131dbc518ad0a4e205']
num = ['1' * 24 + '0' * (79 - 24), '0' * 24 + '1' * 24 + '0' * (79 - 24 * 2), '0' * (24 * 2) + '1' * 24 + '0' * (79 - 24 * 3)]
for a in num:
assert len(a) == 79
cnt = 0
while True:
cnt += 1
t = ''
print(cnt)
io = remote('34.70.212.151', 8000)
for i in range(3):
io.sendlineafter(b'first message: ', a1[i])
io.sendlineafter(b'second message: ', b1[i])
io.sendlineafter(b'num: ', str(int(num[i], 2)))
data = int(io.recvline().strip().split(b'Revealing bits : ')[-1])
# print(data)
t += bin(data)[2:][:24]
t = t + '0110000'
assert len(t) == 79
try:
t = long_to_bytes(int(t, 2)).decode()
except UnicodeDecodeError: continue
if len(t) != 10: continue
print(t)
# exit()
io.sendlineafter(b'Can you Guess the secret:', t)
data = io.recvline().decode()
print(data)
if 'flag' in data:
break
if 'Wrong guess. Bye bye!' not in data:
print(data)
break
else:
print("failed")
io.close()
Cái code này mình viết lúc 4 giờ sáng nên nhìn nó ngu điên =))))
- Note: Sau giải mình có biết thêm 1 trò đó chính là chúng ta đi send -1 vào để and bits =))) lúc này thay vì phải làm 3 lần thì có thể làm 1 lần thôi vì -1 & a = a trong python =)))
1
2
3
4
5
6
7
8
9
10
alphanum = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
secret = ''.join(random.choices(alphanum,k=10))
sec_num = bytes_to_long(secret.encode())
num = -1
bit_count = bin(num).count('1')
assert bit_count <= 24
print(sec_num)
print(sec_num&num)
1
2
271064412279359715358026
271064412279359715358026
Vjp pr0 thật sự =))
Curvy Curves
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from Crypto.Util.number import getRandomNBitInteger, bytes_to_long, long_to_bytes
from sage.all import *
# non-residue
D = 136449572493235894105040063345648963382768741227829225155873529439788000141924302071247144068377223170502438469323595278711906213653227972959011573520003821372215616761555719247287249928879121278574549473346526897917771460153933981713383608662604675157541813068900456012262173614716378648849079776150946352466
# redacted
p = "REDACTED"
q = "REDACTED"
# n = p*q
n = 22409692526386997228129877156813506752754387447752717527887987964559571432427892983480051412477389130668335262274931995291504411262883294295070539542625671556700675266826067588284189832712291138415510613208544808040871773692292843299067831286462494693987261585149330989738677007709580904907799587705949221601393
flag = b"flag{REDACTED}"
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, other):
x = (self.x*other.x + D*self.y*other.y)%n
y = (self.y*other.x + self.x*other.y)%n
return Point(x, y)
def __mul__(self, d):
Q = Point(1, 0)
P = Point(self.x, self.y)
while d != 0:
if d&1 == 1:
Q += P
P += P
d >>= 1
return Q
def __str__(self) -> str:
return f"{self.x}, {self.y}"
def check_residue(y):
if pow(y, (p - 1)//2, p) == 1 and pow(y, (q - 1)//2, q) == 1:
return True
return False
def gen_point():
while True:
x = getRandomNBitInteger(1023 - 240)
x = bytes_to_long(flag + long_to_bytes(x))
x %= n
y2 = ((x*x - 1)*pow(D, -1, n))%n
if(check_residue(y2)):
yp = pow(y2, (p + 1) // 4, p)
yq = pow(y2, (q + 1) // 4, q)
y = crt([yp, yq], [p, q])
return Point(x, y)
M = gen_point()
e = 65537
C = M*e
print(C)
# Cx = 10800064805285540717966506671755608695842888167470823375167618999987859282439818341340065691157186820773262778917703163576074192246707402694994764789796637450974439232033955461105503709247073521710698748730331929281150539060841390912041191898310821665024428887410019391364779755961320507576829130434805472435025, Cy = 2768587745458504508888671295007858261576650648888677215556202595582810243646501012099700700934297424175692110043143649129142339125437893189997882008360626232164112542648695106763870768328088062485508904856696799117514392142656010321241751972060171400632856162388575536779942744760787860721273632723718380811912
Đầu tiên mình đi xác định xem con flag nằm ở chỗ nào rồi sẽ đi ngược từ đó.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def gen_point():
while True:
x = getRandomNBitInteger(1023 - 240)
x = bytes_to_long(flag + long_to_bytes(x))
x %= n
y2 = ((x*x - 1)*pow(D, -1, n))%n
if(check_residue(y2)):
yp = pow(y2, (p + 1) // 4, p)
yq = pow(y2, (q + 1) // 4, q)
y = crt([yp, yq], [p, q])
return Point(x, y)
M = gen_point()
e = 65537
C = M*e
print(C)
Oke, vậy là ban đầu người ta sẽ tạo ra một điểm $M(x_M, y_M)$ thuộc cái curve gì đấy mà mình chưa đọc, trong đó $x$ sẽ chứa flag. Người ta đưa mình điểm $C= e * M$ với $ e = 65537$. Đề bài nghe rất Elliptic Curve nhưng script thì lại rất RSA =)))). Và như mình đã nói ở bài PRSA, khi gặp những bài như thế này thì chúng ta nên đi xác định xem cái nhóm mà chúng ta đang làm việc là nhóm gì, có order như thế nào từ đó ta có thể truy ngược lại $M$ từ $C$.
1
2
# non-residue
D = 136449572493235894105040063345648963382768741227829225155873529439788000141924302071247144068377223170502438469323595278711906213653227972959011573520003821372215616761555719247287249928879121278574549473346526897917771460153933981713383608662604675157541813068900456012262173614716378648849079776150946352466
Mình không hiểu sao nhưng mỗi lần mình thấy đề bài mà có con $D$ như trên thì mình luôn nghĩ tới phương trình Pell, và mình có biết một vài bài có isomorphism từ một đường cong $E$ sang một đường cong gồm các nghiệm của phương trình Pell có order là $p+1$. Cộng thêm việc đề bài có đề cập đến smooth. Mình đã đoán rằng $n = p * q$ với $(p + 1)$ smooth. Lúc này mình đã thử dùng thuật toán William p+1 để factor $n$…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from primefac import *
D = 136449572493235894105040063345648963382768741227829225155873529439788000141924302071247144068377223170502438469323595278711906213653227972959011573520003821372215616761555719247287249928879121278574549473346526897917771460153933981713383608662604675157541813068900456012262173614716378648849079776150946352466
n = 22409692526386997228129877156813506752754387447752717527887987964559571432427892983480051412477389130668335262274931995291504411262883294295070539542625671556700675266826067588284189832712291138415510613208544808040871773692292843299067831286462494693987261585149330989738677007709580904907799587705949221601393
p = williams_pp1(n)
q = n // p
assert p * q == n
print(p)
Và kết quả là….
p = 1779816733304736381084864812803761214302272494619817595962262887353495881068607828373749191179960417738609613170856737290048073479147894242862637932199748403
Nó ra thật =)))
1
2
3
sage: p = 1779816733304736381084864812803761214302272494619817595962262887353495881068607828373749191179960417738609613170856737290048073479147894242862637932199748403
sage: factor(p+1)
2^2 * 268547 * 271969 * 274213 * 287501 * 294181 * 304357 * 306517 * 309433 * 320209 * 333491 * 337277 * 341953 * 351587 * 351749 * 354139 * 379133 * 386651 * 387253 * 395849 * 409523 * 414503 * 448013 * 449629 * 454609 * 455899 * 461323 * 470153 * 488407
Như các bạn có thể thấy, $(p+1)$ smooth như cái cách mà mình tuột khỏi bảng xếp hạng top 10
Sau đó thì mình check được order dưới mod p là (p + 1) và tương tự với mod q, do đó mình lại sử dụng CRT để tìm lại x trong mod n và lấy flag thôi. Bài troll
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *
from primefac import *
from sage.all import *
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, other):
x = (self.x*other.x + D*self.y*other.y)%n
y = (self.y*other.x + self.x*other.y)%n
return Point(x, y)
def __mul__(self, d):
Q = Point(1, 0)
P = Point(self.x, self.y)
while d != 0:
if d&1 == 1:
Q += P
P += P
d >>= 1
return Q
def __str__(self) -> str:
return f"{self.x}, {self.y}"
D = 136449572493235894105040063345648963382768741227829225155873529439788000141924302071247144068377223170502438469323595278711906213653227972959011573520003821372215616761555719247287249928879121278574549473346526897917771460153933981713383608662604675157541813068900456012262173614716378648849079776150946352466
n = 22409692526386997228129877156813506752754387447752717527887987964559571432427892983480051412477389130668335262274931995291504411262883294295070539542625671556700675266826067588284189832712291138415510613208544808040871773692292843299067831286462494693987261585149330989738677007709580904907799587705949221601393
p = 1779816733304736381084864812803761214302272494619817595962262887353495881068607828373749191179960417738609613170856737290048073479147894242862637932199748403
q = n // p
assert p * q == n
t = crt([p + 1, q + 1], [p, q])
Cx = 10800064805285540717966506671755608695842888167470823375167618999987859282439818341340065691157186820773262778917703163576074192246707402694994764789796637450974439232033955461105503709247073521710698748730331929281150539060841390912041191898310821665024428887410019391364779755961320507576829130434805472435025
Cy = 2768587745458504508888671295007858261576650648888677215556202595582810243646501012099700700934297424175692110043143649129142339125437893189997882008360626232164112542648695106763870768328088062485508904856696799117514392142656010321241751972060171400632856162388575536779942744760787860721273632723718380811912
e = 65537
C = Point(Cx, Cy)
xp = (C * pow(e, -1, p + 1)).x
xq = (C * pow(e, -1, q + 1)).x
x = crt([xp, xq], [p, q])
print(long_to_bytes(x))
# flag{pHUCk_150M0rPh15m_1n70_p2}
- Note: Sau khi CTF kết thúc, mình nhận ra có vài người đã giải bài này bằng cách dùng factordb để factor $n$. Có vẻ như có ai đó đã factor $n$ vài phút sau khi CTF bắt đầu và đưa lên database của factordb =)))).
Safe Curvy Curve
Đây là version tiếp theo của bài trước, cùng mình xem nó khác gì nhé
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
from Crypto.Util.number import getPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
from sage.all import *
n = 325325755182481058670589439237195225483797901549838835146388756505962515992731682902174843378473793118013824587686743801443229435097379024643408429957717590072275498734396840489261986361764935791083084431387935565119970246214821662977047205360090509590387268197591520307878877103247121412898793371812283196864079961633428662039795223806526580626911586062085681619829271800589543048515261459541945856915535056363750996243146294104205192635607675773145823355324367791593757860302117944097894321078809559514655550115178790472355420484756646090492860950760854985816746318432545157312928351659730275368368710393481
# non-residue
D = 104195424559311137181271279442498654957365659039072230133307906910289876977215387204406606621273182995744469913980318794193540266885069529501579897759819085330481440863835062469771268905581027223137570462332151650553239341513789960350350245008144164176339007365876329719830893966710072622193879546377346644622
# redacted
p = "REDACTED"
q = n // p
flag = b"REDACTED"
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, other):
x = (self.x*other.x + D*self.y*other.y)%n
y = (self.y*other.x + self.x*other.y)%n
return Point(x, y)
def __mul__(self, d):
Q = Point(1, 0)
P = Point(self.x, self.y)
while d != 0:
if d&1 == 1:
Q += P
P += P
d >>= 1
return Q
def __str__(self) -> str:
return f"{self.x}, {self.y}"
def check_residue(y):
if pow(y, (p - 1)//2, p) == 1 and pow(y, (q - 1)//2, q) == 1:
return True
return False
def gen_point():
while True:
x = getRandomNBitInteger(2000 - 464)
x = bytes_to_long(flag + long_to_bytes(x))
x %= n
y2 = ((x*x - 1)*pow(D, -1, n))%n
if(check_residue(y2)):
yp = pow(y2, (p + 1) // 4, p)
yq = pow(y2, (q + 1) // 4, q)
y = crt([yp, yq], [p, q])
return Point(x, y)
def add(a, b):
if a == "i":
return b
return (D + a*b)*pow(a + b, - 1, n)%n
def power(a, d):
res = "i"
x = a
while d != 0:
if d&1 == 1:
res = add(res, x)
x = add(x, x)
d >>= 1
return res
def point(m):
return Point((m**2 + D)*pow(m**2 - D, -1, n)%n, 2*m*pow(m*m - D, -1, n)%n)
M = gen_point()
Mx, My = M.x, M.y
assert (Mx**2 - D*My**2)%n == 1
e = 65537
C = M*e
print(C)
# 162961013908573567883708515220539578804107270477973090499542519193835498763624042601337274226440312066476160075983577251445943502548471650694617020354363039427231006183897304593798946447482514180041848851245384617847515040075915213698357885114317390276898478740949700799011676589252761736123613456698426984426140183972297018822418150981970598934664464599487393545946613698687046341448558294255407327000026161574779286948527797313848936686929888861150592859573221003557737086661845641459024783317432643308034709718127845066442672512067552552244030535478274512743971354192981490674475749853430371212307520421190, 239668740066200913943562381887193634676899220686058888912170632953311361194017666904277854011894382855202483252661143091091993190645295938873381009873178536800816517615786834926664362950059833369410239281041504946121643304746955139178731148307192034732522723412439705530514113775245607466575056817920259552225402143084439183697819510515790086246564683416312338905722676300264277098153045593619223527605305078928548583405756368607546463429755374790443440435124030514385157787083987202901009878849122637030860266764644062073632184729561756322435322264642199576207018861730005366413597578298926774145872631956206
Hmm…Các bạn có biết nó khác gì không
Mình cũng không biết nữa =))) mình thấy nó lại xuất hiện phương trình Pell này =))
assert (Mx**2 - D*My**2)%n == 1
Mình thử lại code cũ xem nó có ra không…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
n = 325325755182481058670589439237195225483797901549838835146388756505962515992731682902174843378473793118013824587686743801443229435097379024643408429957717590072275498734396840489261986361764935791083084431387935565119970246214821662977047205360090509590387268197591520307878877103247121412898793371812283196864079961633428662039795223806526580626911586062085681619829271800589543048515261459541945856915535056363750996243146294104205192635607675773145823355324367791593757860302117944097894321078809559514655550115178790472355420484756646090492860950760854985816746318432545157312928351659730275368368710393481
p = williams_pp1(n)
q = n // p
assert p * q == n
D = 104195424559311137181271279442498654957365659039072230133307906910289876977215387204406606621273182995744469913980318794193540266885069529501579897759819085330481440863835062469771268905581027223137570462332151650553239341513789960350350245008144164176339007365876329719830893966710072622193879546377346644622
e = 65537
Cx, Cy = 162961013908573567883708515220539578804107270477973090499542519193835498763624042601337274226440312066476160075983577251445943502548471650694617020354363039427231006183897304593798946447482514180041848851245384617847515040075915213698357885114317390276898478740949700799011676589252761736123613456698426984426140183972297018822418150981970598934664464599487393545946613698687046341448558294255407327000026161574779286948527797313848936686929888861150592859573221003557737086661845641459024783317432643308034709718127845066442672512067552552244030535478274512743971354192981490674475749853430371212307520421190, 239668740066200913943562381887193634676899220686058888912170632953311361194017666904277854011894382855202483252661143091091993190645295938873381009873178536800816517615786834926664362950059833369410239281041504946121643304746955139178731148307192034732522723412439705530514113775245607466575056817920259552225402143084439183697819510515790086246564683416312338905722676300264277098153045593619223527605305078928548583405756368607546463429755374790443440435124030514385157787083987202901009878849122637030860266764644062073632184729561756322435322264642199576207018861730005366413597578298926774145872631956206
C = Point(Cx, Cy)
xp = (C * pow(e, -1, p + 1)).x
xq = (C * pow(e, -1, q + 1)).x
x = crt([xp, xq], [p, q])
print(long_to_bytes(x))
# flag{p+1_factor_AND_150M0rPh15m_1n70_p2}
Code mình chả khác gì bài trước, chỉ thay đổi $n$, $D$, $C$ thôi
Thêm một lần hụt first blood
Thế thì chịu lmao
Secure Matrix Transmissions
Nghe tên là biết sắp phải làm việc với ma trận òi
Script đề bài:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
from sage.all import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import random
import os
import hashlib
from base64 import b64encode, b64decode
FLAG = b'flag{REDACTED}' ## removed the flag
f = open('./intercepted.txt', 'w')
p = 33184772290615481426295675425316668758122179640330548849957081783509
N = 6
gl = GL(N, GF(p))
secret = matrix(gl.random_element())
secret_inv = secret ** (-1)
def encrypt(flag, shared_secret):
i = 0
key = 0
for row in shared_secret:
for item in row:
key += item ** i
i += 1
key = hashlib.sha256(long_to_bytes(int(key))).digest()
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
encrypted_text = cipher.encrypt(pad(flag, AES.block_size))
return b64encode(iv + encrypted_text).decode("utf-8")
def decrypt(cipher, shared_secret):
iv, enc = b64decode(cipher)[:16], b64decode(cipher)[16:]
i = 0
key = 0
for row in shared_secret:
for item in row:
key += item**i
i += 1
key = hashlib.sha256(long_to_bytes(int(key))).digest()
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(enc)
return unpad(flag, AES.block_size)
def secure_key_gen():
temp = zero_matrix(GF(p), N)
for i in range(N):
temp[i, i] = random.randint(1, p - 1)
return temp
def gen_params():
A = matrix(gl.random_element())
B = matrix(gl.random_element())
while A.det() == 0 or B.det() == 0:
A = matrix(gl.random_element())
B = matrix(gl.random_element())
f.write(f"A = \n{A}\n") ## intercepted successfully!
f.write(f"B = \n{B}\n") ## intercepted successfully!
return A, B
## generate public parameters
A, B = gen_params()
## for Alice
a = secure_key_gen()
## Sends to Bob
u = secret_inv * A * secret * a * secret_inv * A ** (-1) * secret
f.write(f"u = \n{u}\n") ## intercepted successfully!
## for Bob
b = secure_key_gen()
a_ = secret_inv * A ** (-1) * secret * u * secret_inv * A * secret
key_b = a_ + b
## Sends to Alice
v = secret_inv * B * secret * b * secret_inv * B ** (-1) * secret
f.write(f"v = \n{v}\n") ## intercepted successfully!
## for Alice
b_ = secret_inv * B ** (-1) * secret * v * secret_inv * B * secret
key_a = b_ + a
## Sends to Bob
ct1 = encrypt(b'send me the flag', key_a)
f.write(f"ct1 = {ct1}\n") ## intercepted successfully!
## for Bob
f.write(f"{decrypt(ct1, key_b).decode()}\n")
## Sends to Alice
ct2 = encrypt(FLAG, key_b)
f.write(f"ct2 = {ct2}\n") ## intercepted successfully!
## Read the Flag
# f.write(decrypt(ct2, key_a).decode())
Các bạn thấy dòng cuối của đề bài không f.write(decrypt(ct2, key_a).decode()). Đây cũng chính là mục tiêu của tụi mình.
Bây giờ ct2 thì đề bài đã cho rồi, vậy thì mình cũng nhau xem key_a là gì
key_a = b_ + a với b_ = secret_inv * B ** (-1) * secret * v * secret_inv * B * secret và a = secure_key_gen()
Thường mà trong CTF mình thấy hàm nào có chữ secure là mình nghi ngờ lắm =)). Nên mình sẽ đi xem a là gì trước
1
2
3
4
5
def secure_key_gen():
temp = zero_matrix(GF(p), N)
for i in range(N):
temp[i, i] = random.randint(1, p - 1)
return temp
Hmm ok, có vẻ a là một ma trận đường chéo $6\times6$ trong $GF(p)$. Chưa có vẻ gì là sus lắm, mình tiếp tục xem tiếp đề bài.
Do là chúng ta muốn tìm được key_a thì phải tìm được a nên mình xem những gì liên quan đến a mà mình biết. Ở đây ta có u = secret_inv * A * secret * a * secret_inv * A ** (-1) * secret với u, A được cho trước. Nếu mình nhìn kỹ 1 chút và viết lại secret_inv * A * secret = M_a thì secret_inv * A ** (-1) * secret chính là M_a ** (-1) tức ma trận nghịch đảo của ma trận M_a. Lúc này mình có thể viết lại
Với a là một ma trận đường chéo. Lúc này mình đã ra được ý tưởng làm bài bởi vì công thức trên chính là Jordan form của u
Rồi a có vẻ mình sẽ tìm được…bây giờ thử coi b_ là gì
b_ = secret_inv * B ** (-1) * secret * v * secret_inv * B * secret
Do v mình đã được đề cho rồi nên nếu ta thay v = secret_inv * B * secret * b * secret_inv * B ** (-1) * secret vào b_ thì thấy b_ = b luôn mà b cũng được gen như a vậy là mình chỉ cần đổi Jordan form là xong bài
Hoặc là không =))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
p = 17
N = 4
gl = GL(N, GF(p))
secret = matrix(gl.random_element())
secret_inv = secret ** (-1)
A, B = gen_params()
a = secure_key_gen()
b = secure_key_gen()
u = secret_inv * A * secret * a * secret_inv * A ** (-1) * secret
v = secret_inv * B * secret * b * secret_inv * B ** (-1) * secret
Ju, Pu = u.jordan_form(transformation = True)
Jv, Pv = v.jordan_form(transformation = True)
border = '-' * 100
print(f"want a: \n{a}")
print(border)
print(f"test a: \n{Ju}")
print(border)
print(f"want b: \n{b}")
print(border)
print(f"test b: \n{Jv}")
Mình thử tự gen số nhỏ để test ý tưởng trước
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
want a:
[12 0 0 0]
[ 0 9 0 0]
[ 0 0 3 0]
[ 0 0 0 13]
----------------------------------------------------------------------------------------------------
test a:
[13| 0| 0| 0]
[--+--+--+--]
[ 0|12| 0| 0]
[--+--+--+--]
[ 0| 0| 9| 0]
[--+--+--+--]
[ 0| 0| 0| 3]
----------------------------------------------------------------------------------------------------
want b:
[15 0 0 0]
[ 0 10 0 0]
[ 0 0 1 0]
[ 0 0 0 13]
----------------------------------------------------------------------------------------------------
test b:
[15| 0| 0| 0]
[--+--+--+--]
[ 0|13| 0| 0]
[--+--+--+--]
[ 0| 0|10| 0]
[--+--+--+--]
[ 0| 0| 0| 1]
Để ý thấy thì ma trận a, b mình tự tính hơi khác cái đã được gen ở chỗ là nó đã được sort giảm dần trên cái đường chéo. Lúc này do thời gian cũng không còn nhiều và mình buồn ngủ =)) nên mình đã hoán vị trên đường chéo của 2 ma trận và test từng cái cho tới khi ra được flag. Điều này hoàn toàn khả thi do ma trận đề bài chỉ là $6 \times 6$ vậy mình chỉ cần khoảng $(6!)^2 + abc$ thao tác với abc là mấy cái thao tác decrypt rồi với vấn gì đấy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
from sage.all import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import random
import os
import hashlib
from base64 import b64encode, b64decode
p = 33184772290615481426295675425316668758122179640330548849957081783509
N = 6
gl = GL(N, GF(p))
def encrypt(flag, shared_secret):
i = 0
key = 0
for row in shared_secret:
for item in row:
key += item ** i
i += 1
key = hashlib.sha256(long_to_bytes(int(key))).digest()
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
encrypted_text = cipher.encrypt(pad(flag, AES.block_size))
return b64encode(iv + encrypted_text).decode("utf-8")
def decrypt(cipher, shared_secret):
iv, enc = b64decode(cipher)[:16], b64decode(cipher)[16:]
i = 0
key = 0
for row in shared_secret:
for item in row:
key += item**i
i += 1
key = hashlib.sha256(long_to_bytes(int(key))).digest()
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(enc)
# print(flag)
return flag
u = [
[28879155726567049983454622837721881713004421469649633653126003880251, 22074946600328057026240224251921516029989227864483537878311928528684, 11985344636547053777186855301874485401032363227366605932898421631165, 11038047153398875511855062921770308445072978178537727544345865556069, 17913589562779438181451311229483343663752773108623377725718452883819, 6988548052196701160389870027180255419046432117124570998462066223760],
[12442646139394994295898159421691536460921770233410583384741128805851, 26791343238957883953511341730456926026845067572390616134588257575715, 20044295739622127408570744416765049400182932494144906328843165683951, 3716946288972247122675229801442487271330697050902983897960257015353, 28203806658422488413821254734838742146597120966298092240011671950418, 4762041594051527320517864505450207655232589320366293231953595725863],
[30088717492536940712495821833412730937575223939046572858904284613916, 27041904353687235206996420047457376344449825180129098056224307456338, 24437749819141358658247648214143755332360241994475937257542642573583, 7796437298901905297245658644368499053223939852560146715778064632640, 15614447029063100426172954288407641313530323021423668136405899310194, 8922479681646925758338291598256040373376681973788891756406422763139],
[19322178296033807354940969679463195308540921806504252678149867173138, 33097125072731086770607131468725547500825910975790412321782115869838, 12883750093703623804432147375290510155697961091062129358847651674123, 24597869343287697641622709721671426915780058312255624403180234192713, 26537027184297668426345397663386813121592656652583736980586291216445, 11617206120365401967915791192731000879817682674901777733903856797733],
[16710090447056060108731601191705411717377136736726300253063986063308, 13112164116392985346393033303671764991807289870465207976284880921022, 31389068001989884948885767386697332939461030078718007394707803846255, 29908327338977214304615826417150579857655888232250984362081852839023, 22583975168456327742148140296560922679546031771450762766874213823663, 20255781234412108781956807555843619052915858233204195711555194680279],
[ 8639975336305093270106069074993623126891247360031281653825740040741, 13403900498226599196478196563037659383351290165716358605156795361654, 19127443140313962513371049800518743806366324348931149667137542330176 , 1587790520831406950292877253889772565635165863077419349924612463554, 28260643245678615796033409984375030239968039321917236595612922928109, 27245620107342379746895845516019185969531890676595911744377909557532]]
v = [
[14593469507593520336534893606693100073219081551387449023943771554442, 2283021458111487923710380205365151066104282754263745192237326490551, 13170584523093998223191696419879547969801075848834311698387381471505, 19259980148204759114097202057965316584985415828667111050145931544542, 29885290219184042616179535742918968947354026457415023160998318453828, 15123772566136939254700272466681741447495954560621338927076401710465],
[8217862512033149496876384094296269532452490863111766288591338421520, 13729461020836068836298855334139849351346259147300854170266838049852, 11104728330778098008854657250493837339864716593096275438194673593723, 10798384644614928362418932155290042574495162355923347471159291144698, 31877189181091302604647976237742181979760578672930582051196549136046, 1918629350716436456009684853559872579413764560427000121836347921516],
[17260689732862422635435505221480922746751317064535215923993790192886, 15747877220363614821162725299191209258209710570887630567232690904197, 8617228034985901541131740069450254422228498135170302566742947957775, 14253933715820016671570267997896238444667901637428211288460788838246, 16499164346493998999442730191394982099986918128009049722691512093014, 13025912772710188038104092079604197742726564877681113284285303849554],
[ 2573456644853874338239370492651477088261797251129609392543920453838, 32896562598550390417662631073664427877599458467029721692315947839203, 21609625125792777949315379171355985793236349536655762275501735276637, 2064423690239912348059209794358643838603106021323566574579622769345, 10416995935649914543433851087690149206442589809600595549054529630023, 14743736977132006506906381861127077616280508458806441865058344748656],
[ 4225662325959455234970599933733361974460852167061568484358345163405, 10702969665926869787857799410201005975577054702738405546384443139142, 1359255767431309667828876308576650892896838633542052871017414741807, 31671777458706492709787940377250078973397972903701973598970849268174, 24125683246160911728533816896560068159204522435801109506125539244342, 6566591950072749090239378195580530026605442552103644998279546358496],
[ 2340617144223968993993626239720251771746071020532956496851092249201, 18464940637598472739277490361512029859881180718968424684424994902717, 27460971987555371094455429952593747078655439217048574014441041685569, 6667117338244005137290181664972559554258953283885089203943302963181, 20312635823091168798778853401004417385080412291250382174823545520392, 32296141232133239312731746201245526393343079356560448241095997297137]]
ct1 = 't22qVcUY/TYh9hwuASW/6PliQ03dLEWpOTqZHF82rQ/VqmqX7fj2l1YHzX7Cq0Sy'
ct2 = '8t5wC5gsdXOG7vDvw+uStOT1P2ZhB2FGsr/lvNaBMX+FAZ9aVY4UMOk8neL3KcELjQ3F62aX/sxN4KexO/krK2mm/v10qYrKbLPXljdwvck='
u = matrix(gl(u))
v = matrix(gl(v))
Ju, Pu = u.jordan_form(transformation = True)
Jv, Pv = v.jordan_form(transformation = True)
def get_per(a, permu):
b = zero_matrix(GF(p), N)
for i in range(len(permu)):
b[i, i] = a[permu[i], permu[i]]
return matrix(gl(b))
import itertools
per = list(itertools.permutations(range(int(6)), int(6)))
from tqdm import tqdm
while True:
for p1 in tqdm(per):
cur_ju = get_per(Ju, p1)
for p2 in per[::-1]:
cur_jv = get_per(Jv, p2)
key_a = cur_ju + cur_jv
f = decrypt(ct2, key_a)
if b'flag' in f:
print(f)
exit()
# flag{In53cUr3_K3Y_3xch4ng3_0n_n0n-4b3L14n_gR0up5!!}
Mình đi ăn sáng với bạn, về nhà là lấy flag (khoảng 2 tiếng)
Rebellious
Tiếp tục 1 bài Elliptic Curve
Script đề bài
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from sage.all import *
from Crypto.Util.number import *
import random
import time
random.seed(time.time())
FLAG = b'flag{REDACTED}' ## flag removed
flag = bytes_to_long(FLAG)
f = open('./output.txt', 'w')
p = 2653051169113192956861029164111253541045934291082610203810454254019428617095444726883436858598608538656059147405437762506043477080240989129049112094108099635297397071457202368492446105766960803000479292350528610656494430695078098921185726745996662867511185527654339397
F = GF(p)
a, b = random.randint(2, p), random.randint(2, p)
f.write(f"a = {a}\nb = {b}")
def point_addition(px, py, qx, qy):
rx = F((pow(a, -1, p) * (px * qx - py * qy * (a ** 2) * (pow(b ** 2, - 1, p)))) % p)
ry = F((pow(a, -1, p) * (px * qy + py * qx)) % p)
return (rx, ry)
def scalar_multiplication(px, py, k):
rx = a
ry = 0
while k:
if k % 2:
rx, ry = point_addition(rx, ry, px, py)
px, py = point_addition(px, py, px, py)
k >>= 1
return rx, ry
G = generator_curve() ## implementation hidden for enhancing security
x1 = G[0]
y1 = G[1]
H = scalar(multiplication(x1, y1, flag))
x2 = H[0]
y2 = H[1]
f.write(f"x1 = {x1}\n")
f.write(f"y1 = {y1}\n")
f.write(f"x2 = {x2}\n")
f.write(f"y2 = {y2}\n")
Đầu tiên là mình xác định flag nằm ở đâu
$ H = flag * G$
Với $H, G$ là $2$ điểm thuộc curve cho trước. Vậy đây là 1 bài DLP trong 1 cái group nào đấy. Thông thường cách mình tiếp cận những bài này sẽ là tìm một cái isomorphism sang một cái group khác mà việc giải DLP trên group mới dễ dành hơn so với group ban đầu. Vậy thế nào là dễ dàng? Mình thì chỉ biết làm DLP khi order smooth thôi nên mình cố gắng kiếm cái group nào mà có order như vậy.
Mình check $p-1$ thì thấy nó khá smooth:
1
2
3
sage: p = 2653051169113192956861029164111253541045934291082610203810454254019428617095444726883436858598608538656059147405437762506043477080240989129049112094108099635297397071457202368492446105766960803000479292350528610656494430695078098921185726745996662867511185527654339397
sage: factor(p-1)
2^2 * 2199768451 * 2523276191 * 2674991047 * 2737748831 * 3017308807 * 3074323591 * 3116578807 * 3169245991 * 3210267583 * 3218788571 * 3326149831 * 3346140859 * 3353408659 * 3355659943 * 3366693263 * 3388813691 * 3398273927 * 3463644143 * 3736045787 * 3745049927 * 3781238647 * 3803691487 * 3954763051 * 4038986663 * 4193283007 * 4196830147 * 4254066703 * 4258097359
Vậy lúc này mình sẽ cố gắng đi tìm $\phi$ là một isomorphism từ $F_p \times F_p$ $\rightarrow F_p$ (do $F_p$ có order là $(p - 1)$ smooth)
Đây cũng chính là phần quan trọng của bài này. Tới đây thì mình chỉ làm việc với giấy trắng và bút chì thôi. Vậy thì mình cần nháp cái gì?
Để dễ hình dung nhất thì mình đã thử $(x, y) + (x, y) = ???$
Dựa vào script của đề bài
1
2
3
4
def point_addition(px, py, qx, qy):
rx = F((pow(a, -1, p) * (px * qx - py * qy * (a ** 2) * (pow(b ** 2, - 1, p)))) % p)
ry = F((pow(a, -1, p) * (px * qy + py * qx)) % p)
return (rx, ry)
Viết ra thì mình thấy
$(x, y) + (x, y) = (a^{-1}(x^2 - y^2 a^2 b^{-2}), a^{-1}2xy)$
Để tiện nhìn thì mình sẽ thay $D = -a^2b^{-2}$. Lúc này mình có
$(x, y) + (x, y) = (a^{-1}(x^2 + Dy^2), a^{-1}2xy)$
Có phải tới đây nếu bạn lấy $x + \sqrt{D}y$ thì nó sẽ ra được hàng đẳng thức không? Cụ thể là
\[x + \sqrt{D}y = a^{-1} (x^2 + 2\sqrt{D}xy + Dy^2) = a^{-1}(x + \sqrt{D}y)^2\]Công thức này nhìn có vẻ đẹp. Vậy chúng ta có thể lấy $\phi(x,y) = x + \sqrt{D}y$ không?
Để trả lời câu hỏi này thì chúng ta sẽ cần phải check xem:
$\phi((x, y) + (x, y)) = \phi(x,y) * \phi(x,y)$ ?
Ở công thức trước thì mình đa biết vế trái = $a^{-1}(x + \sqrt{D}y)^2$
Còn vế phải thì sẽ là $(x + \sqrt{D}y) * (x + \sqrt{D}y) = (x + \sqrt{D}y)^2$
Rõ ràng vế trái $\neq$ vế phải. Tuy nhiên khác này không nhiều mình hoàn toàn có thể thêm $a^{-1}$ vào $\phi$, khi này $\phi = a^{-1}(x + \sqrt{D}y)$. Khi check lại $\phi((x, y) + (x, y)) = \phi(x,y) * \phi(x,y)$ thì chúng ta sẽ thấy vế trái $=$ vế phải $= a^{-2}(x+\sqrt{D}y)^2$
Vậy là mình đã có thể map sang $F_p$ để dễ dàng solve DLP hơn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from sage.all import *
a = 896628675751371304018467516533039804176775933799175745538502687106559694221345569606835023924573486284340033527118135205049330439505968603591951157299842692320540140045548212956876194361589003179447395457270969770617973628611227780145733474250476117969057162498481006
b = 1594141190031606167637964033584529087047496888670585921966214269273813000209103412838275833742634054062344129649888363945908517421292739690476942454492374399040827799113145071785163083279816370591990677345359419792838696359950227158548645341674614589920736730841882901
x1 = 2447311429245810608453598977721926525743937062790274783828355485892913926324404325450262209205021127183454615611616550259333401589502955319014494993678853183049373710785536450442318295835466655474548890496853017541519682383303084185775030215811426581216914216950270956
y1 = 410833649474095008286303725355620198973100699243884756648778973683976772919818182547446663925208006608569743058617356228744003207376383969798498652649980419669823060847067368605737714840647452806304738527797730984565975278507624074132585153613359147658622391652166219
x2 = 1566139005633252473556201451242364632915578424632734493066937660397101401569493967529787221059042873428725135212835566524682514836524110403515558447949858337441010924644644029611890576656944925197135969895065157485428935029723186607110153424152429492883484492551653983
y2 = 2465843379413974191156984954011192642764891821373485281212757233528541318669422125099128501651227153989791786833109663869690960602895820768585534236263284886527281849932400111969526972107723029072948750348496980814617349507385444584704833764454106237879211652308963312
p = 2653051169113192956861029164111253541045934291082610203810454254019428617095444726883436858598608538656059147405437762506043477080240989129049112094108099635297397071457202368492446105766960803000479292350528610656494430695078098921185726745996662867511185527654339397
F = GF(p)
dd = -1 * (a ** 2) * (pow(b ** 2, - 1, p)) % p
d_ = F(dd).sqrt()
assert pow(d_, 2, p) == dd
def f(x, y):
return pow(a, -1, p) * (x + d_ * y) % p
g = F(f(x1, y1))
h = F(f(x2, y2))
o = discrete_log(h, g)
print(long_to_bytes(o).decode())
# flag{gR0uP_150M0rPH15m5_4R3_g0NN4_b3_7h3_3nD_0f_y0Ur_L1f3!}

-lmaoooo.png)