LACTF2024

Last weekend, I participated in the lactf with team blackpinker. We achieved the 31st position overall. This article will cover the write-ups of the crypto challenges in the competition. It’s quite unfortunate that we couldn’t solve the final challenge during the contest, but overall, it was a fun CTF and we learned a lot.

valentines-day

Based on the description, there are some keywords we need to pay attention to.

Vigenere cipher: the method of encryption

161 characters long: the key’s length

And of course the flag format

Before delving into additional information from external sources, we will examine the files provided by the challenge.

Intro

On this Valentine's day, I wanted to show my love for professor Paul Eggert. This challenge is dedicated to him. Enjoy the challenge!

Ciphertext

Br olzy Jnyetbdrc'g xun, V avrkkr gb sssp km frja sbv kvflsffoi Jnuc Sathrg. Wkmk gytjzyakz mj jsqvcmtoh rc bkd. Canjc kns puadlctus!

L xyw fmoxztu va tai szt, dbiazb yiff mt Zzhbo 1178 gyfyjhuzw vhtkqfy sniu eih vbsel edih tpcvftz, xcie ysnecsmge hbucqtu qt wcorr crzhg-olhm srr gkh gdsjxqh gnxxl rtr guez jewr klkkgak dx uuka nnv hmvwbj gmv glz fvyh, jueg eww oq i wuqglh Z lrigjsss ynch xun esivmpwf: "oof hvrb frtbrq it Kcmlo?"

C ltzihfvxsq ghp abqs qrfzf glvx de HN bnty gocr gr:

Eiaj zek rvocf vnriiu ob Puiza. Xegjy webrvbvrj. Frat s vgxhidm kepldrv gbq phxgv.

Ehlb'w wuhu C ixyzchlr, ilc srez foq e wxzb sdz nrbrb. Eej W und siieesx nd pvvgb zvr pooi. B fox wc nrax v pedgei aex phvqe. Hqdru pc tvvtrv, C zyoxvxsq ghq wyvbg yzgmex KEKN=/ife/lgcyr/qg/ejl:$TNXC, eej hurn mlp qowtswvqn:

wrm ~cuamyh/umlofikjayrvplzcwm.gdg | pzwj
ropgf{qvjal_dfuxaxzbk_gbq_jeci_hdt_nr_hdr_eexij}

...

I will use the cipher’s algebraic description to tackle the challenge

According to the description, decrypting the ciphertext to find the flag requires rediscovering the key. This is the moment when we make use of the hint provided by the challenge.

We can partially recover the key as follow:

\[K_i = C_i - M_i \pmod{26}\]

Where C is the first paragraph of the ciphertext and M our Intro

enc = "Br olzy Jnyetbdrc'g xun, V avrkkr gb sssp km frja sbv kvflsffoi Jnuc Sathrg. Wkmk gytjzyakz mj jsqvcmtoh rc bkd. Canjc kns puadlctus!"
pt = "On this Valentine's day, I wanted to show my love for professor Paul Eggert. This challenge is dedicated to him. Enjoy the challenge!"

d = [chr(i) for i in range(ord('A'), ord('Z') + 1)]

import string 
s = string.ascii_letters

key = ""

for i, c in enumerate(enc): 
    if c not in s: continue # We only encrypting ascii letters
    char = d[(ord(c) - ord(pt[i])) % 26]
    key += char  

print(f"partial key: {key}")
print(f"length: {len(key)}")

partial key: NEVERGONNAGIVEYOUUPNEVERGONNALETYOUDOWNNEVERGONNARUNAROUNDANDDESERTYOUNEVERGONNAMAKEYOUCRYNEVERGONNASAYGOO
length: 106

We all know where this is going. But first, we will attempt to use the obtained key fragment to see if we can recover the flag.

unknown = '\0' * (161 - len(key))

test_key = key + unknown # Making the key 161 characters long

with open('./enc.txt') as f:
    enc = f.read()

enc = enc.upper()

test = ""

idx = 0
ldx = 0

for idx in range(len(enc)):
    if enc[idx] not in s: test += enc[idx] 
    else: test += d[(ord(enc[idx]) - ord(test_key[ldx % len(test_key)])) % 26]; ldx += 1 

print(test)

We did manage to find our flag despite not knowing the last 55 characters of the original key.

ON THIS VALENTINE'S DAY, I WANTED TO SHOW MY LOVE FOR PROFESSOR PAUL EGGERT. THIS CHALLENGE IS DEDICATED TO HIM. ENJOY THE CHALLENGE!

Y KLJ SZBKMGH IN GNV FMG, QOVNMO LVSS ZG MMUOB 1178 TLSLWUHMJ IUGXDSL FAVH AND EVERY EXAM PROBLEM, THEN SEARCHING THROUGH MY SLIDE PRINT-OUTS FOR THE CLOSEST MATCH AND THEN JUST WRITING IT DOWN AND HOPINW TZI TYM SILU, WHRT RJJ BD V JHDTYU M YEVTWFFF LAPU KHA RFVIZCJS: "BBS UING BANNED IN CHINA?"

I REMEMBERED THE WISE WORDS THAT MY TA ONCE TOLD ME:

BING WAS NEVER BANNED IN CHINA. NAIVE UNDERGRAD. RENT A VIRTUQZ XRCYQEI TOD CUKTI.

RUYO'J JHUH P VKLMPUYE, VYP FERM SBD R JKMO FQM AEONG. AND I HAD MANAGED TO CRACK THE CODE. I HAD TO RENT A LNXSRV AND CHECK. UNDER MY BREATH, I MUTTERED THE WORDS EXPORT PATH=/USR/LOCAL/CS/RWY:$GAKP, RRW UHEA ZYC DBJGFJIDA:

JEZ ~PHNZLU/HZYBSVXWNLEICYMPJZ.TQT | LESS
LACTF{KNOWN_PLAINTEXT_AND_WERE_OFF_TO_THE_RACES}

Remember our flag format contains not upper but lower case letters. So our final flag is:

lactf{known_plaintext_and_were_off_to_the_races}

very-hot

RSA: a public-key cryptosystem

Let’s examine the files provided by the challenge.

Challenge’s script

from Crypto.Util.number import getPrime, isPrime, bytes_to_long
from flag import FLAG

FLAG = bytes_to_long(FLAG.encode())

p = getPrime(384)
while(not isPrime(p + 6) or not isPrime(p + 12)):
    p = getPrime(384)
q = p + 6
r = p + 12

n = p * q * r
e = 2**16 + 1
ct = pow(FLAG, e, n)

print(f'n: {n}')
print(f'e: {e}')
print(f'ct: {ct}')

To decrypt in RSA, we need the private exponent d, which satisfies the equation $ed \equiv 1 \pmod{\phi(n)}$ where $\phi$ is Euler’s totient function. To find d, we need to find the prime factors of n, then compute $e^{-1} \pmod{\phi(n)}$. This is why factoring large numbers is one of the mathematical challenges on which the security of the RSA cryptosystem relies.

Looking back at the script, the prime numbers used in the problem were created in an insecure manner for RSA encryption. We can factorize n as follow:

1. Construct $f(x) = x(x + 6)(x + 12) - n$

2. Find the roots of $f(x) = 0$, notice that $x = p$ is a solution to the equation.

3. Once $p$ is determined, $q$ and $r$ can be calculated. Thus completing the factorization of n.

from Crypto.Util.number import * 
from sage.all import * 

n = 10565111742779621369865244442986012561396692673454910362609046015925986143478477636135123823568238799221073736640238782018226118947815621060733362956285282617024125831451239252829020159808921127494956720795643829784184023834660903398677823590748068165468077222708643934113813031996923649853965683973247210221430589980477793099978524923475037870799

F = PolynomialRing(ZZ, 'x')

x = F.gen()

f = x * (x + 6) * (x + 12) - n

p = ZZ(f.roots()[-1][0])
q = p + 6 
r = p + 12 

assert p * q * r == n 

Once the fatorization of $n$ is done, we derive $\phi(n)$ using the formula $\phi(n) = (p - 1) (q - 1) (r - 1)$. With $\phi(n)$, we can compute the private exponent $d$. Then, by evaluating $ct^d \equiv m^{ed} \equiv m \pmod{n}$, we decrypt the ciphertext to obtain our flag.

phi = (p - 1) * (q - 1) * (r - 1)

e = 2**16 + 1

d = pow(e, -1, phi)

ct = 9953835612864168958493881125012168733523409382351354854632430461608351532481509658102591265243759698363517384998445400450605072899351246319609602750009384658165461577933077010367041079697256427873608015844538854795998933587082438951814536702595878846142644494615211280580559681850168231137824062612646010487818329823551577905707110039178482377985

flag = long_to_bytes(pow(ct, d, n))

print(flag)

# lactf{th4t_w45_n0t_so_53xY}

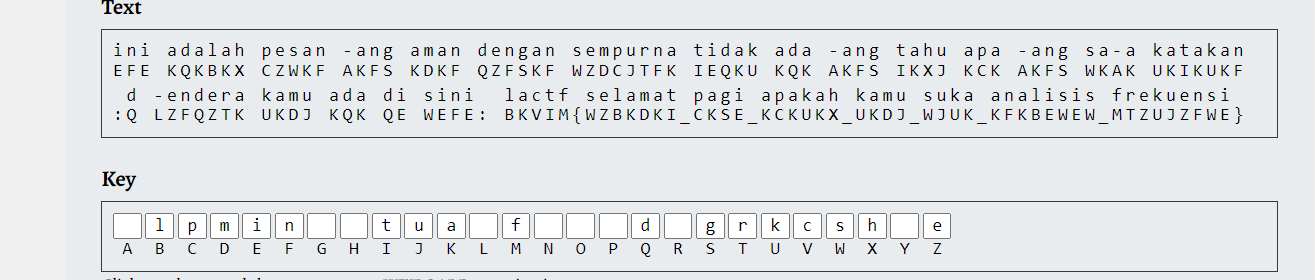
selamat pagi

The challenge was solved by one of my teammates, Dat2Phit.

The message looks like this:

Efe kqkbkx czwkf akfs kdkf qzfskf wzdcjtfk
Ieqku kqk akfs ikxj kck akfs wkak ukikukf :Q
Lzfqztk ukdj kqk qe wefe: bkvim{wzbkdki_ckse_kckukx_ukdj_wjuk_kfkbewew_mtzujzfwe}

Our approach was to use Frequency analysis. That is to count the frequency of ciphertext letters and then associate guessed plaintext letters with them along with some Google translation. We found a letter frequencies of the langague Indonesian online and proceeded to guess the keys by trial and error. Notice that we can immediately replace b -> l, k -> a, …. since our flag format is lactf{...}.

Final flag: lactf{selamat_pagi_apakah_kamu_suka_analisis_frekuensi}

which translates to good_morning_do_you_like_frequency_analysis

Yes.

h0lyT

There’s not much information about the challenge in the description, so let’s examine our server’s script.

Challenge’s script

from Crypto.Util.number import getPrime, bytes_to_long
import random
def legendre(a, p):
    return pow(a, (p - 1) // 2, p)

def tonelli(n, p):
    q = p - 1
    s = 0
    while q % 2 == 0:
        q //= 2
        s += 1
    if s == 1:
        return pow(n, (p + 1) // 4, p)
    for z in range(2, p):
        if p - 1 == legendre(z, p):
            break
    c = pow(z, q, p)
    r = pow(n, (q + 1) // 2, p)
    t = pow(n, q, p)
    m = s
    t2 = 0
    while (t - 1) % p != 0:
        t2 = (t * t) % p
        for i in range(1, m):
            if (t2 - 1) % p == 0:
                break
            t2 = (t2 * t2) % p
        b = pow(c, 1 << (m - i - 1), p)
        r = (r * b) % p
        c = (b * b) % p
        t = (t * c) % p
        m = i
    return r
def xgcd(a, b): 
    if a == 0 : 
        return 0,1
             
    x1,y1 = xgcd(b%a, a) 
    x = y1 - (b//a) * x1 
    y = x1 
     
    return x,y 
def crt(a, b, m, n):
    m1, n1 = xgcd(m, n)
    return ((b *m * m1 + a *n*n1) % (m * n))

def advice(x, p, q):
    if legendre(x, p) != 1:
        exit()
    if legendre(x, q) != 1:
        exit()
    x1 = tonelli(x, p) * random.choice([1, -1])
    x2 = tonelli(x, q) * random.choice([1, -1])
    y = crt(x1, x2, p, q)
    return y
    
def main():
    p = getPrime(1024)
    q = getPrime(1024)
    N = p * q
    e = 65537
    m = bytes_to_long(b"lactf{redacted?}")
    ct = pow(m, e, N)
    print(f"ct = {ct}")
    print(f"N = {N}")
    print(f"e = {e}")
    while 1:
        x = int(input("What do you want to ask? > "))
        ad = advice(x, p, q)
        print(ad)

if __name__ == "__main__":
    main()

The task presents a challenging script that may seem daunting initially. However, I’ll provide a concise summary:

1. The server is using RSA to encrypt the flag
2. We are given $ciphertext$, $e$, $N$. Addtionally, we are able to ask infinitely many time the square root of $x$ in modulo $N$.
3. Our goal is to decrypt the ciphertext and recover the flag.

Using the knowledge of the square root of x modulo N, we can factorize N in the following manner:

1. Find $x_1$, $x_2$ such that $x_1^2 \equiv x_2^2 \equiv x \pmod{N}$ and $x_1 \not\equiv \pm x_2 \pmod{N}$
2. Computes $GCD(x-y, N)$ will give us the factors of $N$

To understand why this works, we notice that:

\[\begin{aligned} &x_1^2 \equiv x_2^2 \pmod{N} \\ \Leftrightarrow &x_1^2 - x_2^2 \equiv 0 \pmod{N} \\ \Leftrightarrow &(x_1 - x_2)(x_1 + x_2) \equiv 0 \pmod{N} \end{aligned}\]

The second condition guarantees that $N$ does not divide $(x_1 + x_2)$ nor $(x_1 − x_2)$ individually. Thus we have found factors of $N$ ($p$ and $q$ in our case).

This is also known as Congruence of squares.

from pwn import * 
from Crypto.Util.number import * 

host, port = 'chall.lac.tf', 31171

io = remote(host, port)

ct = int(io.readline().split(b' = ')[-1].decode())

N = int(io.readline().split(b' = ')[-1].decode())

e = 65537

io.sendlineafter(b'What do you want to ask? >', '100') # 100 for let's make this year 100% our best year? :) 

x1 = int(io.recvline())

x2 = x1 

while x2 == x1:
    io.sendlineafter(b'What do you want to ask? >', '100')
    x2 = int(io.recvline())

p = GCD(x1 - x2, N)

q = N // p 

assert p * q == N 

Similar to the previous challenge, after obtaining the factors of N, decrypting and retrieving the flag becomes trivial.

d = pow(e, -1, (p-1) * (q-1))
flag = pow(ct, d, N)

print(long_to_bytes(flag))

io.interactive()

# lactf{1s_r4bin_g0d?}

That’s interesting, I didn’t think about Rabin’s cryptosystem at all.

prove it!

Initially, I was a bit worried about the challenge description as it led me to think about zk-SNARKs, which is something I find quite vague. But after some time examining the challenge’s script, it turned out not to be so bad.

Challenge’s script

#!/usr/local/bin/python
import random

flag = "lactf{??????????}"
p = 171687271187362402858253153317226779412519708415758861260173615154794651529095285554559087769129718750696204276854381696836947720354758929262422945910586370154930700427498878225153794722572909742395687687136063410003254320613429926120729809300639276228416026933793038009939497928563523775713932771366072739767


if __name__ == "__main__":
    
    s = random.getrandbits(128)
    alpha = random.getrandbits(40)
    g = redacted
    ss = [pow(g, s**i, p) for i in range(1,8)]
    alphas = [pow(g, alpha * s**i, p) for i in range(1,8)]
    print(f"Use these values to evaluate your polynomials on s")
    print(f"Powers of s: {ss}")
    print(f"Powers of alpha*s: {alphas}")
    tries = 0
    while True:
        if tries >= 2:
            print("Fool me once shame on you, fool me twice shame on me")
            break
        print("Can you prove to me you know the polynomial f that im thinking of?")
        target = []
        for i in range(8):
            target.append(random.randrange(p))
        print(f"Coefficients of target polynomial: {target}")
        ts = sum([(pow(s,7 - i, p) * target[i]) % p for i in range(len(target))]) % p
        f = int(input("give me your evaluation of f(s) > ")) % p
        h = int(input("give me your evaluation of h(s) > ")) % p
        fa = int(input("give me your evaluation of f(alpha * s) > ")) % p
        if f <= 1 or h <= 1 or fa <=1 or f == p-1 or h == p-1 or fa == p-1:
            print("nope")
            exit()
            
        if pow(f, alpha, p) != fa or f != pow(h, ts, p):
            print(f"failed! The target was {ts}")
            tries += 1
            continue

        print(f"you made it! here you got {flag}")
        break

Note: all of the calculation below will be done in $\Z_p$ if not stated otherwise.

Let’s summarize the challenge:

We are given:

$ss = {g^s, g^{s^2}, \dots, g^{s^7}}$

$alphas = {g^{\alpha s}, g^{\alpha s^2}, \dots, g^{\alpha s^7}}$

In order to get the flag, we have to provide $f$, $h$, $fa$ such that $fa = f^\alpha$ and $f = h^{ts}$ in 2 tries, where $ts = t_7 + s^1 t_6 + \dots + s^7 t_0$. We are also given ${t_0, t_1, \dots, t_7}$.

Our strategy for tackling this challenge involved identifying $\alpha$ and $s$. Subsequently, we are able to calculate our custom $f$, $h$, and $fa$ that fulfill the given condition.

Notice that:

\[\begin{aligned} \log_{g^s}{g^{\alpha s}} &= \log_{g^s}{(g^s)^\alpha} \\ &= \alpha \log_{g^s}{g^s} \\ &= \alpha \end{aligned}\]

But we are not in $\R$ but rather in $\Z_p$. This is also known as Discrete logarithm.

Since $ord(\Z_p)= p - 1$ we can attempt to factorize $p - 1$ to determine if it is smooth enough for us to perform discrete logarithm using Pohlig–Hellman algorithm.

I used factordb to factor $p - 1$

from random import getrandbits, randrange
from sage.all import *
from pwn import *

p = 171687271187362402858253153317226779412519708415758861260173615154794651529095285554559087769129718750696204276854381696836947720354758929262422945910586370154930700427498878225153794722572909742395687687136063410003254320613429926120729809300639276228416026933793038009939497928563523775713932771366072739767
factor = [2, 7, 13, 19, 53, 1777, 13873, 375066324492304430531233, 101314441051291953151795913529403295472268626955749910388589943712415215415423242460768521635363326511421993561697020926882352863815817760585519668584579396434359231480732446870758449266392982408911461909631947699423464740818101880230788267861965299542533361995389464266063]
assert prod(factor) + 1 == p 

The first $7$ factors are quite small. Hopefully, their product is sufficient for 40 bits to fully recover $\alpha$ since $\alpha$ is $40$ bits long.

print(prod(factor[:7]).bit_length()) # 43

Nice, now we can recover $\alpha$.

host, port = 'chall.lac.tf', 31179

io = remote(host, port)

io.recvuntil(b'Powers of s: ')

ss = eval(io.recvline())

assert len(ss) == 7

io.recvuntil(b'Powers of alpha*s: ')

alphas = eval(io.recvline())

assert len(alphas) == 7

io.recvuntil('Coefficients of target polynomial: ')

target = eval(io.recvline())

assert len(target) == 8 

subresults = []
factors = []
modulus = 1

max_val = 2 ** 40

order = p - 1

for prime in factor:
    if modulus >= max_val: break
    _factor = prime ** 1
    factors.append(_factor)
    a = pow(ss[0], order//_factor, p)
    b = pow(alphas[0], order//_factor, p)
    modulus *= _factor
    subresults.append(discrete_log(GF(p)(b), GF(p)(a), ord = modulus))

alpha = crt(subresults,factors)

for i, x in enumerate(ss):
    assert pow(x, alpha, p) == alphas[i]

Can we do the same to recover $s$? Well…, I’m not quite sure. Since $s$ is $128$ bits long, I think it would take too long, unless there’s some magical function in Sage that can computes this in no time.

But remember that we have 2 tries, there must be another way to recover $s$. Let’s denote ${ts}_i$ as the value of $ts$ for the $i$-th try.

if pow(f, alpha, p) != fa or f != pow(h, ts, p):
    print(f"failed! The target was {ts}")
    tries += 1
    continue

The server actually tells us ${ts}_1$, enabling us to recover as follow:

1. Construct $g(x) = t_7 + t_6 x + \dots + t_0 x^7 - {ts}_1$, where $t_i$ is the our first try’s coefficients of target polynomial.
2. Find the roots of $g(x) = 0$, notice that $x = s$ is a solution to the equation.

io.sendlineafter(b"give me your evaluation of f(s) > ", '2')
io.sendlineafter(b"give me your evaluation of h(s) > ", '2')
io.sendlineafter(b"give me your evaluation of f(alpha * s) > ", '2')

io.recvuntil(b'failed! The target was ')

ts = int(io.recvline())

F = PolynomialRing(GF(p), 'x')

x = F.gen()

f = F(0)

for i in range(len(target)):
    f += F(x ** (7 - i)) * target[i]

f -= ts

s = ZZ(f.roots()[-1][0])

Now we are able to calculate our custom $f$, $h$, and $fa$.

io.recvuntil('Coefficients of target polynomial: ')

target = eval(io.recvline())

assert len(target) == 8 

ts = sum([(pow(s,7 - i, p) * target[i]) % p for i in range(len(target))]) % p

h = 2
f = pow(h, ts, p) 
fa = pow(f, alpha, p)

io.sendlineafter(b"give me your evaluation of f(s) > ", str(f))
io.sendlineafter(b"give me your evaluation of h(s) > ", str(h))
io.sendlineafter("give me your evaluation of f(alpha * s) > ", str(fa))

# lactf{2kp_1s_ov3rr4t3d}

io.interactive()

budget-bag

Reading the description, we can get an idea of the challenge’s content, it’s related to Knapsack cryptosystems. Let’s take a look at the challenge’s script.

import random
from hidden import DollarStore
p = 95773813056613526295315889615423014145567365190638271416026411091272805051097
def legendre(a, p):
    return pow(a, (p - 1) // 2, p)

def tonelli(n, p):
    q = p - 1
    s = 0
    while q % 2 == 0:
        q //= 2
        s += 1
    if s == 1:
        return pow(n, (p + 1) // 4, p)
    for z in range(2, p):
        if p - 1 == legendre(z, p):
            break
    c = pow(z, q, p)
    r = pow(n, (q + 1) // 2, p)
    t = pow(n, q, p)
    m = s
    t2 = 0
    while (t - 1) % p != 0:
        t2 = (t * t) % p
        for i in range(1, m):
            if (t2 - 1) % p == 0:
                break
            t2 = (t2 * t2) % p
        b = pow(c, 1 << (m - i - 1), p)
        r = (r * b) % p
        c = (b * b) % p
        t = (t * c) % p
        m = i
    return r
class EllipticCurve:
    def __init__ (self, a, b, p):
        self.p = p
        self.a = a
        self.b = b
    def getPoint(self, x):
        ys = (x**3 + self.a*x + self.b) % p
        if legendre(ys, self.p) != 1:
            return None
        y = tonelli( ys ,p)
        return CurvePoint(x, y, self)
    
class CurvePoint:
    def __init__(self,x,y, curve):
        self.curve = curve
        self.x = x % curve.p
        self.y = y % curve.p
    def __str__(self):
        return f"({self.x},{self.y})"
    def __eq__(self, other):
        return str(self) == str(other)
    __repr__ = __str__
    def __add__(self, other):
        x1,y1 = self.x, self.y
        x2,y2 = other.x, other.y
        if x2 == 0 and y2 == 1:
            return self
        if x1 == 0 and y1 == 1:
            return other
        if x1 == x2 and y2 == self.curve.p - y1:
            return CurvePoint(0, 1, self.curve)
        if x1 == x2 and y1 == y2:
            lam = ((3*pow(x1, 2, self.curve.p) + self.curve.a) * pow(2* y1, -1, self.curve.p))% self.curve.p
        else:
            lam = ((y2 - y1) * pow(x2 - x1, -1, self.curve.p)) % self.curve.p
        x = (lam**2 - x1 - x2) % self.curve.p
        y = (lam*(x1 -x) - y1) % self.curve.p
        return CurvePoint(x, y, self.curve)


def scalar_mult(x, n, ec) -> CurvePoint:
    Q = x
    R = CurvePoint(0,1 ,ec)
    if n == 0: return R
    if n == 1: return x
    while n > 0:
        if n % 2 == 1:
            R = R + Q
        Q = Q + Q
        n = n // 2
    return R

flag = "lactf{REDACTED}" 

flag = flag.lstrip("lactf{").rstrip("}")

flagarray = [((random.randrange(2**10) >> 8) << 8) + ord(flag[i]) for i in range(len(flag))]

ec = DollarStore()

points = []
while len(points) < len(flagarray):
    x = random.randrange(p)
    point = ec.getPoint(x)
    if point != None:
        points.append(point)

s = scalar_mult(points[0], flagarray[0], ec)
for i in range(1,len(flagarray)):
    s += (scalar_mult(points[i], flagarray[i], ec))

print(f"s= {s}")

print(f"points = {points}")

To summarize the main points of the challenge:

We are given:

The points ${G_0, G_1, \dots, G_n}$ where each point $G_i(x_i, y_i)$ is a point on the curve $y_i^2 \equiv x^3 + ax + b \pmod{p}$

$s = m_0 G_0 + m_1 G_1 + \dots + m_n G_n$ where $m_i$ is the character of the flag.

If these weren’t points on the Elliptic Curve, we can simply use the low density attack which is constructing a lattice basis $M$:

\[\begin{aligned} M = \left(\begin{array}{cc} G_0 & 1 & 0 & \dots & 0 & 0\\ G_1 & 0 & 1 & \dots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots &\vdots\\ G_n & 0 & 0 & \dots & 1 & 0\\ s & 0 & 0 & \dots & 0 & 1 \\ p & 0 & 0 & \dots & 0 & 0 \end{array}\right) \end{aligned}\]

Perform LLL on $M$ and find our small target vector $x = (0, m_0, m_1, …, -1)$ with the linear combination $t = (m_0, m_1, …, -1, k)$.

But since it’s arithmetic on the curve, we can’t directly use this method, let’s actually understand what curve we are on by finding $a$ and $b$

We can use any $2$ points $G_i$ and $G_j$ ($i \not= j$) to do this. Notice that we have:

\[\begin{aligned} \begin{cases} y_0^2 \equiv x_0^3 + ax_0 + b \pmod{p} &(1)\\ y_1^2 \equiv x_1^3 + ax_1 + b \pmod{p} &(2) \end{cases} \end{aligned}\]

$(1) - (2)$ gives us the equation $y_0^2 - y_1^2 \equiv x_0^3 - x_1^3 + a(x_0 - x_1) \pmod{p}$

$\Rightarrow a \equiv ((y_0^2 - y_1^2) - (x_0^3 - x_1^3))(x_0 - x_1)^{-1} \pmod{p}$

We can then substitute $x_0$, $y_0$, $a$ into $(1)$ to calculate $b$

p = 95773813056613526295315889615423014145567365190638271416026411091272805051097
G0 = (48868244275342945713292068450286493306842109652612873048852850861527337784625, 8598765896895208028227058726713353098258128734049351946507804225327296634514)
G1 = (72658254142472216221352003377742816858998248904595208415554148006123670275598, 71428807550814004521976397789820845661680868197262344890701351814974388342261)

a = (G0[1] ** 2 - G1[1] ** 2) - (G0[0] ** 3 - G1[0] ** 3) 
a *= pow(G0[0] - G1[0], -1, p) 
a %= p 

b = (G0[1] ** 2 - G0[0] ** 3 - a * G0[0]) % p 

print(f"a: {a}")
print(f"b: {b}")

a: 0
b: 0

That’s interesting. Since $a = b = 0$, our curve becomes $y^2 = x^3$

This is a singular curve which has a group isomorphism as follow:

For anyone who is enthusiastic about the theorem’s proof: Elliptic Curves Number Theory and Cryptography

The field $K$ in our context is $\Z_p$ with opperator of addition. Now we don’t have to work on the curve anymore, we can map it to $\Z_p$ and construct our lattice basis $M$ as:

\[\begin{aligned} M = \left(\begin{array}{cc} x_0y_0^{-1} & 1 & 0 & \dots & 0 & 0\\ x_1y_1^{-1} & 0 & 1 & \dots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots &\vdots\\ x_ny_n^{-1} & 0 & 0 & \dots & 1 & 0\\ x_sy_s^{-1} & 0 & 0 & \dots & 0 & 1 \\ p & 0 & 0 & \dots & 0 & 0 \end{array}\right) \end{aligned}\]

from sage.all import *
p = 95773813056613526295315889615423014145567365190638271416026411091272805051097

def f(x, y):
    return (x * pow(y, -1, p)) % p 

s= (4690331917760414380672348505790486524786128272326163170078478915876334878778,77902523131087061897126273610460347147805642819184490444996378236375931739511)

points = ...

a = [f(x, y) for (x, y) in points]

s = [f(s[0], s[1])]

mat = column_matrix(ZZ, a + s)

mat = mat.augment(identity_matrix(len(a) + 1))

mat = mat.stack(vector([p] + [0] * (len(a) + 1)))

lll = mat.LLL()

for r in lll.rows():
    if r[0] == 0:
        x = [-1 * r[-1] * a for a in r[1:-1]]
        x = [chr(k - (k // 256 * 256)) for k in x]
        flag = 'lactf{' + ''.join(x) + '}'
        print(flag)
        exit()

# lactf{im_w4y_t00_br0k3!}

shuffle

This challenge was solved by one of my teammates, naul. I will briefly go through the idea of the solution.

Challenge’s script

#!/usr/local/bin/python3

from secrets import randbits
import math
from base64 import b64encode
MESSAGE_LENGTH = 617

class LCG:

    def __init__(self,a,c,m,seed):
        self.a = a
        self.c = c
        self.m = m
        self.state = seed

    def next(self):
        self.state = (self.a * self.state + self.c) % self.m
        return self.state

def generate_random_quad():
    return randbits(64),randbits(64),randbits(64),randbits(64)

initial_iters = randbits(16)

def encrypt_msg(msg, params):
    global initial_iters
    a, c, m, seed = params
    L = LCG(a, c, m, seed)
    for i in range(initial_iters):
        L.next()
    l = len(msg)
    permutation = []
    chosen_nums = set()
    while len(permutation) < l:
        pos = L.next() % l
        if pos not in chosen_nums:
            permutation.append(pos)
            chosen_nums.add(pos)
    output = ''.join([msg[i] for i in permutation])
    return output

# period is necessary
secret = b64encode(open('secret_message.txt','rb').read().strip()).decode() + '.'
length = len(secret)
assert(length == MESSAGE_LENGTH)

a, c, m, seed = params = generate_random_quad()
enc_secret = encrypt_msg(secret,params)

while True:
    choice = input("What do you want to do?\n1: Shuffle a message.\n2: Get the encrypted secret.\n3: Quit.\n> ")
    if choice == "1":
        message = input("Ok. What do you have to say?\n")
        if (len(message) >= length):
            print("I ain't reading allat.\n")
        elif (math.gcd(len(message),m) != 1):
            print("Are you trying to hack me?\n")
        else:
            print(f"Here you go: {encrypt_msg(message,params)}\n")
    elif choice == "2":
        print(f"Here you go: {enc_secret}\n")
    elif choice == "3":
        print("bye bye")
        exit(0)
    else:
        print("Bad choice.\n")

The challenge is using a LCG to permute the characters of the flag. The “L” in LCG means linear so as long as we know the states and it’s parameters, we can reverse the encryption process and capture the flag.

    while len(permutation) < l:
        pos = L.next() % l
        if pos not in chosen_nums:
            permutation.append(pos)
            chosen_nums.add(pos)
    output = ''.join([msg[i] for i in permutation])
    return output

Unfortunately, we don’t have full knowledge of the state itself but rather the the state modulo by l where l is the length of the message that we want to encrypt (make sure that GCD(l, 617) == 1).

We can still recover the state however, by collecting enough state % l, we can use Chinese remainder theorem to hopefully recover the $64$ bits long state.

from pwn import *
from Crypto.Util.number import isPrime, GCD
from tqdm import tqdm
from math import prod
from sympy.ntheory.modular import crt
from sage.all import matrix, Integers, vector

STR = bytes([i for i in range(0x30, 256)])

c = remote('chall.lac.tf', 31172)
c.sendlineafter('> ', '2')
encrypted_text = c.recvline()
print(encrypted_text)
enc = encrypted_text[encrypted_text.index(b':') + 2 : -1]
modulus = []
moduli = []
results = []

i_vals = [i for i in range(71, len(STR)) if isPrime(i) and GCD(i, 617) == 1]
for i in tqdm(i_vals): 
    c.sendlineafter('> ', '1')
    c.sendlineafter('?\n', STR[:i])
    modulus.append(i)
    result = c.recvline()
    result = result[result.index(b':') + 2: -1]
    results.append(result)
    assert len(result) == i
    if prod(modulus).bit_length() > 64:
        break

print(prod(modulus).bit_length(), modulus)

We deliberately selected a starting value of $71$ for our modulus to ensure that the prod(modulus).bit_length() approaches $64$ as closely as possible. This increases our chances of success in identifying the states.

65 [71, 73, 79, 83, 89, 97, 101, 103, 107, 109]

states = []
for position in range(10):
    moduli = []
    for result in results:
        moduli.append(STR.index(result[position]))
    states.append(crt(modulus, moduli)[0])

# Checking if we got the correct states 
for i, state in enumerate(states):
    if state.bit_length() > 64 and i < 6:
        raise Exception 

All that’s left to do is findind the LCG’s parameters which are a, c, m

It is done as follow (the post):

We will have to check if our candidate for m is $64$ bits long.

ts = [states[i+1] - states[i] for i in range(len(states) - 1)]
u = [ts[i+2] * ts[i] - ts[i+1] * ts[i+1] for i in range(len(ts) - 2)]

if GCD(u[0], u[1]).bit_length() == 64:
    m = GCD(u[0], u[1])
    a = [[states[0], 1], [states[1], 1]]
    b = [states[1], states[2]]
    a = matrix(Integers(m), a)
    b = vector(Integers(m), b)
    x, y = a.solve_right(b)
    x, y = int(x), int(y)

Now we can do the whole encryption process again to know where the original index got mapped to.

l = len(enc)
permutation = []
chosen_nums = set()
while len(permutation) < l:
    pos = state % l
    if pos not in chosen_nums:
        permutation.append(pos)
        chosen_nums.add(pos)
    state = (x * state + y) % m
inverse = [permutation.index(i) for i in range(len(enc))]
assert len(inverse) == 617
pt = ''.join([enc[inverse[i]] for i in range(len(enc))])
from base64 import b64decode
print(b64decode(pt[:-1]).decode())

"""
I just invented the best shuffling algorithm!
Nobody can read this!
Here, let me hide a flag here: lactf{th3_h0us3_c0uld_n3v3r_l0se_r1ght}
I better not see anyone try to lay their three fingers sideways (mod m) and declare "with this breath, I determine a to be congruent to (X_2 - X_3)/(X_2 - X_1) and c to be trivial"
I mean, it's surely impossible to decipher this message right
I'm going to sell this algorithm to every casino ever and get rich mwahahahaha
"""

Our flag is: lactf{th3_h0us3_c0uld_n3v3r_l0se_r1ght}

pprngc

This challenge is about PRNG.

#!/usr/local/bin/python3

import secrets
from super_secret_stuff import flag, f, f_inverse

seed = secrets.randbits(16)
function_uses = 0
oracle_uses = 0
done = False

def compute_output_bit(state, pred):
    return bin((state & pred)).count("1") % 2

def prng(pred):
    cur_state = seed
    outputs = []
    for i in range(16):
        cur_state = f(cur_state)
        outputs.append(compute_output_bit(cur_state, pred))
    cur_state = f(cur_state)
    cur_state_bits = format(cur_state, 'b').zfill(16)
    all_bits = ("".join([str(i) for i in outputs]) + cur_state_bits)[::-1]
    return all_bits

def pprngc(pred, stream):
    state = int("".join(stream[:16][::-1]), 2)
    for i in range(16, len(stream)):
        state = f_inverse(state)
        if not compute_output_bit(state, pred) == int(stream[i]):
            return None
    state = f_inverse(state)
    return compute_output_bit(state, pred)

print("All you need to know about f is that it's a function from 16 bits to 16 bits")
print("The output on today's secret seed is:", f(seed))
if __name__ == "__main__":
    while not done:
        choice = input("What can I do for you? 1. get random bits 2. use f 3. predict next bit 4. guess seed ").strip()
        if choice == "1":
            rand_pred = secrets.randbelow(2**16)
            output = prng(rand_pred)
            print(output)
            print("Using predicate", rand_pred)
            print("Ignore the fact that the first 16 bits are always the same (or don't, your choice)")
        elif choice == "2":
            if function_uses == 15:
                print("Nah, you've had enough.")
                continue
            num = input("Gimme a number! ").strip()
            try:
                num = int(num)
                if num < 0 or num >= 2**16:
                    print("Out of range!")
                else:
                    print(f(num))
                    function_uses += 1
            except:
                print("Uh something went wrong.")
        elif choice == "3":
            if oracle_uses == 16:
                print("Nah, you've had enough.")
                continue
            stream = input("Gimme the bitstream you want to predict! ").strip()
            if len(stream) < 16:
                print("Out of range!")
            else:
                pred = input("Oh, can you also give a predicate with that? ").strip()
                try:
                    pred = int(pred)
                    if pred < 0 or pred >= 2 ** 64:
                        print("Out of range!")
                    else:
                        output = pprngc(pred, stream)
                        if output is None:
                            print("Uh lemme get back to you on that...")
                            print("*liquidates assets, purchases fake identity, buys one way ticket to Brazil*")
                            done = True
                        else:
                            print(output)
                            oracle_uses += 1
                except:
                    print("Uh something went wrong.")
        elif choice == "4":
            guess = input("Well, let's see it! ").strip()
            if str(seed) == guess:
                print(flag)
            else:
                print("Nope! Sorry!")
            done = True
        else:
            print("Buh bye!")
            done = True

It’s a custom prng, our goal is to find seed ($16$ bits long) to get the flag. We will have to fully understand what the program is doing.

Let’s have a look at the function prng:

def prng(pred):
    cur_state = seed
    outputs = []
    for i in range(16):
        cur_state = f(cur_state)
        outputs.append(compute_output_bit(cur_state, pred))
    cur_state = f(cur_state)
    cur_state_bits = format(cur_state, 'b').zfill(16)
    all_bits = ("".join([str(i) for i in outputs]) + cur_state_bits)[::-1]
    return all_bits

The function computes output using the seed as the initial state and pred.When we call the function, it will computes 16 output bits, our state will change each time it computes an output bit. It then return the state and the outputs.

The function used to calculate output:

def compute_output_bit(state, pred):
    return bin((state & pred)).count("1") % 2

The function pprng:

def pprngc(pred, stream):
    state = int("".join(stream[:16][::-1]), 2)
    for i in range(16, len(stream)):
        state = f_inverse(state)
        if not compute_output_bit(state, pred) == int(stream[i]):
            return None
    state = f_inverse(state)
    return compute_output_bit(state, pred)

The function will check if the output is correct, if not it will return None and we won’t be able to communicate with the server anymore. Without this we can give malicious pred and get info about the seed’s bit since the function is calling state = f_inverse(state). If we use prng to get state || output and some preds like 00...01, 00...10, …, 10...0 we can learn all 16 bits of the seed. So is it hopeless?

Luckily, we have 15 times to use the f function and we know f(seed) from the start. What would happen if we call pprngc(pred = 1, stream = f(seed))? The loop won’t run since len(stream) = 16, we will then learn information about the seed’s last bit.

After that, we can use choice 2 to get f(f(seed)), computes our own output bit with pred = 2, create the stream = f(f(seed)) || output. The loop will loop once since our stream now has length = 17, now compute_output_bit(state, pred) == int(stream[i]) will be True because we calculated it ourselves, giving us information about the seed’s next to last bit. Continue this method until we fully recover the seed.

from pwn import * 

host, port = 'chall.lac.tf', 31173

io = remote(host, port)

def compute_output_bit(state, pred):
    return bin((state & pred)).count("1") % 2

io.recvuntil(b"The output on today's secret seed is:")

states = [int(io.recvline())]

for i in range(15):
    io.sendlineafter(b"What can I do for you? 1. get random bits 2. use f 3. predict next bit 4. guess seed ", '2')
    io.sendlineafter(b"Gimme a number! ", str(states[-1]))
    states.append(int(io.recvline()))

s = ''

for i in range(16):
    pred = 1 << i 
    outputs = []
    for j in range(i):
        outputs.append(compute_output_bit(states[j], pred))
    cur_state_bits = format(states[i], 'b').zfill(16)
    all_bits = ("".join([str(i) for i in outputs]) + cur_state_bits)[::-1]
    io.sendlineafter(b"What can I do for you? 1. get random bits 2. use f 3. predict next bit 4. guess seed ", '3')
    io.sendlineafter(b"Gimme the bitstream you want to predict! ", all_bits)
    io.sendlineafter(b"Oh, can you also give a predicate with that? ", str(pred))
    s = io.recvline().strip().decode() + s 
    
io.sendlineafter(b"What can I do for you? 1. get random bits 2. use f 3. predict next bit 4. guess seed ", '4')
io.sendlineafter(b"Well, let's see it! ", str(int(s, 2)))

# lactf{we_love_blum-micali_generators_h1MNZuJSFjlAEwc1}

io.interactive()